Предмет: Алгебра,
автор: ЕкатеринаБелкина
Всем привет помогите выполнить алгебру
Приложения:
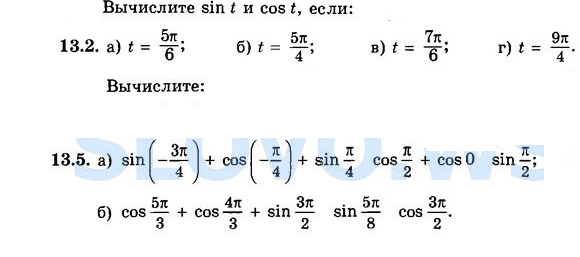
Ответы
Автор ответа:
0
Автор ответа:
0
SIN(5*pi/6)=SIN(pi-pi/6)=sin(pi/6)=1/2= 0,5
COS(5*pi/6)=cos(pi-pi/6)=-cos(pi/6)=-корень(3)/2= -0,86603
SIN(5*pi/4)=SIN(pi+pi/4)=-sin(pi/4)=-корень(2)/2=-0,70711
COS(5*pi/4)=cos(pi+pi/4)=-cos(pi/4)=-корень(2)/2 = -0,70711
SIN(7*pi/6)=SIN(pi+pi/6)=-sin(pi/6)=-1/2= -0,5
COS(7*pi/6)=cos(pi+pi/6)=-cos(pi/6)=-корень(3)/2= -0,86603
SIN(9*pi/4)=SIN(2pi+pi/4)=sin(pi/4)=корень(2)/2 = 0,707107
COS(9*pi/4)=cos(2pi+pi/4)=cos(pi/4)=корень(2)/2 = 0,707107
13.5
непонятно, есть ли знаки умножения, поэтому по 2 решения для 2-х разночтений условия
sin(-3*pi/4)+cos(-pi/4)+sin(pi/4) = -корень(2)/2- корень(2)/2 + корень(2)/2 = 0,707106781
cos(pi/2)+cos(0) = 0+1=1
sin(pi/2)=1
sin(-3*pi/4)+cos(-pi/4)+sin(pi/4)*cos(pi/2)+cos(0)*sin(pi/2)=1
cos(5*pi/3)+cos(4*pi/3)+sin(3*pi/2) = -cos(pi/3)-cos(pi/3)-sin(pi/2)=-1
sin(5*pi/8)=sin(pi-3pi/8)=sin(3*pi/8)=0,923879533
cos(3*pi/2)=0
cos(5*pi/3)+cos(4*pi/3)+sin(3*pi/2)*sin(5*pi/8)*cos(3*pi/2)=0
COS(5*pi/6)=cos(pi-pi/6)=-cos(pi/6)=-корень(3)/2= -0,86603
SIN(5*pi/4)=SIN(pi+pi/4)=-sin(pi/4)=-корень(2)/2=-0,70711
COS(5*pi/4)=cos(pi+pi/4)=-cos(pi/4)=-корень(2)/2 = -0,70711
SIN(7*pi/6)=SIN(pi+pi/6)=-sin(pi/6)=-1/2= -0,5
COS(7*pi/6)=cos(pi+pi/6)=-cos(pi/6)=-корень(3)/2= -0,86603
SIN(9*pi/4)=SIN(2pi+pi/4)=sin(pi/4)=корень(2)/2 = 0,707107
COS(9*pi/4)=cos(2pi+pi/4)=cos(pi/4)=корень(2)/2 = 0,707107
13.5
непонятно, есть ли знаки умножения, поэтому по 2 решения для 2-х разночтений условия
sin(-3*pi/4)+cos(-pi/4)+sin(pi/4) = -корень(2)/2- корень(2)/2 + корень(2)/2 = 0,707106781
cos(pi/2)+cos(0) = 0+1=1
sin(pi/2)=1
sin(-3*pi/4)+cos(-pi/4)+sin(pi/4)*cos(pi/2)+cos(0)*sin(pi/2)=1
cos(5*pi/3)+cos(4*pi/3)+sin(3*pi/2) = -cos(pi/3)-cos(pi/3)-sin(pi/2)=-1
sin(5*pi/8)=sin(pi-3pi/8)=sin(3*pi/8)=0,923879533
cos(3*pi/2)=0
cos(5*pi/3)+cos(4*pi/3)+sin(3*pi/2)*sin(5*pi/8)*cos(3*pi/2)=0
Похожие вопросы
Предмет: Математика,
автор: ndaniil691
Предмет: Қазақ тiлi,
автор: Aluasoft
Предмет: Математика,
автор: dinmuhamed20082008
Предмет: Математика,
автор: ЛЯЛЯЛЯЛЯЛ