Предмет: Алгебра,
автор: HopiTakeo
Решить интеграл ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
Приложения:
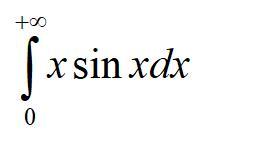
Ответы
Автор ответа:
1
Ответ: интеграл расходится
Похожие вопросы
Предмет: Русский язык,
автор: sergey2130
Предмет: Українська література,
автор: Kristinka150125
Предмет: Русский язык,
автор: Ксюша00000000000001
Предмет: Литература,
автор: katuyschakot
Предмет: История,
автор: Moon19876