Предмет: Алгебра,
автор: HopiTakeo
Решить интеграл ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
Приложения:
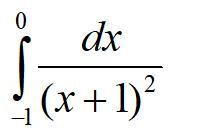
Ответы
Автор ответа:
1
Так как левосторонний и правосторонний пределы различны, предел не существует а поэтому интеграл расходится.
Похожие вопросы
Предмет: Українська література,
автор: Kristinka150125
Предмет: Русский язык,
автор: Ксюша00000000000001
Предмет: Английский язык,
автор: Мариама
Предмет: История,
автор: Moon19876