Реши систему уравнений методом алгебраического сложения.
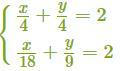
Ответы
Ответ:
Решение системы уравнений х= -20
у=28
Объяснение:
х/4+у/4=2
х/18+у/9=2
Чтобы избавиться от дробного выражения, нужно все части первого уравнения умножить на 4, а все части второго уравнения на 18:
х+у=8
х+2у=36
Смысл метода алгебраического сложения в том, чтобы при сложении уравнений одно неизвестное взаимно уничтожилось. То есть, коэффициенты или при х, или при у были одинаковыми, но с противоположными знаками. Для того, чтобы этого добиться, преобразовывают одно из уравнений, как бы подгоняют ко второму, можно умножать обе части уравнения на одно и то же число, делить.
В данной системе уже есть одинаковые коэффициенты при х, ничего сильно преобразовывать не нужно, но знаки не противоположные, поэтому нужно какое-то из уравнений умножить на -1, например, первое:
-х-у= -8
х+2у=36
Складываем уравнения:
-х+х-у+2у= -8+36
у=28
Теперь значение у подставляем в любое из двух уравнений системы и вычисляем х:
х+2*28=36
х+56=36
х=36-56
х= -20
Решение системы уравнений х= -20
у=28