Предмет: Геометрия,
автор: batoev07
Даю 60 баллов, Доп. задача. №1. Дана окружность с центром О. В данной окружности проведены два диаметра AB и CD. Докажите, что AC=BD. №2. Найдите отрезки касательных AB и AC, проведенных из точки A к окружности радиуса r, если r=9 см, а угол BAC равен 120°. (Пожалуйста с дано, найти, решение. Спасибо!)
Ответы
Автор ответа:
0
Объяснение:
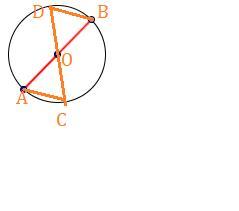
1)Дано окр. О(r) , АВ, СD-диаметры .
Доказать АС=BD
Доказательство.ΔАОС=ΔВОD по двум сторонам и углу между ними : АО=ОВ и СО=ОD как радиусы одной окружности, ∠АОС=∠ВОD как вертикальные .
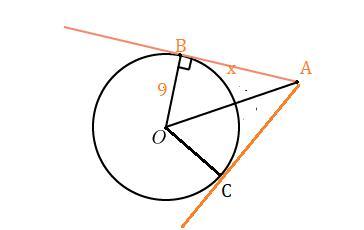
2) Дано окр. О(r) , r=9 см , АВ, АС-касательные, ∠ВАС=120°.
Найти: АВ , АС.
Решение. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания ⇒∠ОВА=∠ОСА=90°. Проведем АО.
Отрезки касательных к окружности, проведенных из одной точки, равны , т.е АВ=АС , и составляют равные углы с прямой, проходящей через эту точку и центр окружности, т.е. ∠ВАО=∠САО=120°:2=60°.
ΔВАО : ∠ВОА=90°-60°=30°. Пусть АВ=х , по св. угла 30° ⇒ОА=2х. По т. Пифагора (2х)²=х²+9² или 3х²=81 или х²=27 или х=3√3. АВ=АС=3√3 см
Приложения:
Похожие вопросы
Предмет: Химия,
автор: artem64rus
Предмет: Математика,
автор: Дашкановичок
Предмет: Русский язык,
автор: linoshkakalinina
Предмет: Математика,
автор: tusya48
Предмет: Физика,
автор: Soloma93