Предмет: Физика,
автор: Soloma93
помогите решить 4 вариант!
Приложения:

Ответы
Автор ответа:
0
1. Заменим распределенную нагрузку равнодействующей:
 =
=  * 5 = 15 * 5 = 75 кН.
* 5 = 15 * 5 = 75 кН.
2. Обозначим опоры "A" и "B".
3. Укажем опорные реакции " " и "
" и " ".
".
4. Составим уравнения равновесия: Σ = 0; Σ
= 0; Σ  = 0.
= 0.
Σ = +
= +  * 3.5 -
* 3.5 -  * 1 -
* 1 -  * 7 -
* 7 -  = 0,
= 0,
 = ( + Fq1 * 3.5 -
= ( + Fq1 * 3.5 -  * 1 -
* 1 -  ) / + 7 = ( + 75 * 3.5 - 10 * 1 - 5) / + 7 = 35.357 кН.
) / + 7 = ( + 75 * 3.5 - 10 * 1 - 5) / + 7 = 35.357 кН.
Σ = -
= -  * 3.5 +
* 3.5 +  * 6 +
* 6 +  * 7 -
* 7 -  = 0,
= 0,
 = ( - Fq1 * 3.5 + F1 * 6 - M1 ) / - 7 = ( - 75 * 3.5 + 10 * 6 - 5) / - 7 = 29.643 кн.
= ( - Fq1 * 3.5 + F1 * 6 - M1 ) / - 7 = ( - 75 * 3.5 + 10 * 6 - 5) / - 7 = 29.643 кн.
5. Выполним проверку, используя уравнение Y = 0:
ΣY = +
+  -
-  +
+  = 0
= 0
ΣY = + 29.643 + 35.357 - 75 + 10 = 0.00
Ответ: = 29.643 кН;
= 29.643 кН;  = 35.357 кН.
= 35.357 кН.
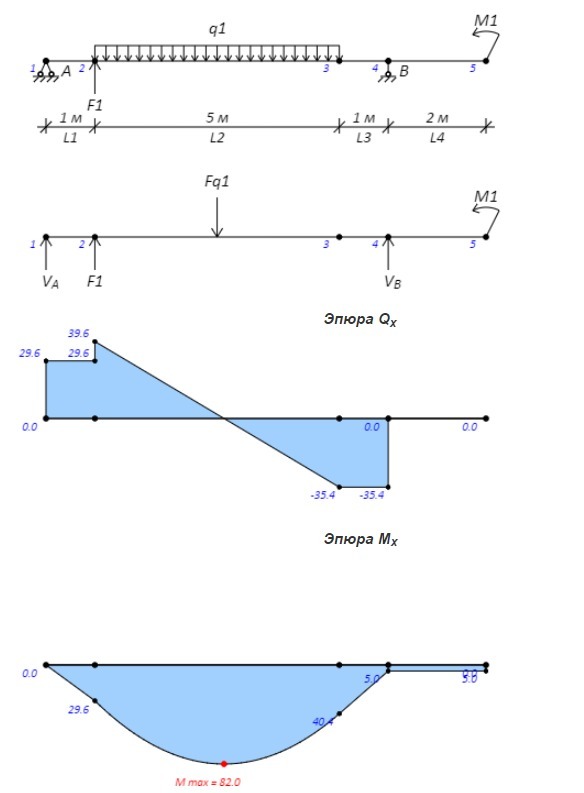
6. Стром эпюру . Определеим значения поперечных сил в характерных сечениях:
. Определеим значения поперечных сил в характерных сечениях:
 лев = 0
лев = 0
 прав = +
прав = +  = + 29.643 = 29.643
= + 29.643 = 29.643
 лев = +
лев = +  = + 29.643 = 29.643
= + 29.643 = 29.643
 прав = +
прав = +  +
+  = + 29.643 + 10 = 39.643
= + 29.643 + 10 = 39.643
 = +
= +  +
+  -
-  = + 29.643 + 10 - 75 = -35.357
= + 29.643 + 10 - 75 = -35.357
 лев = +
лев = +  +
+  -
-  = + 29.643 + 10 - 75 = -35.357
= + 29.643 + 10 - 75 = -35.357
 прав = +
прав = +  +
+  -
-  +
+  = + 29.643 + 10 - 75 + 35.357 = 0
= + 29.643 + 10 - 75 + 35.357 = 0
 = +
= +  +
+  -
-  +
+  = + 29.643 + 10 - 75 + 35.357 = 0
= + 29.643 + 10 - 75 + 35.357 = 0
Эпюра пересекает нулевую линию, определим расстояние от точки 3 до точки пересечения нулевой линии:
пересекает нулевую линию, определим расстояние от точки 3 до точки пересечения нулевой линии:
 = 5 * 39.643 / ( 39.643 + 35.357 ) = 2.64 м.
= 5 * 39.643 / ( 39.643 + 35.357 ) = 2.64 м.
7. Стром эпюру Mx. Определеим изгибающие моменты в характерных точках:
 = 0
= 0
 = +
= +  * 1 = + 29.643 * 1 = 29.643
* 1 = + 29.643 * 1 = 29.643
 = +
= +  * 6 +
* 6 +  * 5 -
* 5 -  * 2.5 = + 29.643 * 6 + 10 * 5 - 75 * 2.5 = 40.358
* 2.5 = + 29.643 * 6 + 10 * 5 - 75 * 2.5 = 40.358
 = +
= +  * 7 +
* 7 +  * 6 -
* 6 -  * 3.5 = + 29.643 * 7 + 10 * 6 - 75 * 3.5 = 5.001
* 3.5 = + 29.643 * 7 + 10 * 6 - 75 * 3.5 = 5.001
 лев = +
лев = +  * 9 +
* 9 +  * 8 -
* 8 -  * 5.5 +
* 5.5 +  * 2 = + 29.643 * 9 + 10 * 8 - 75 * 5.5 + 35.357 * 2 = 5.001
* 2 = + 29.643 * 9 + 10 * 8 - 75 * 5.5 + 35.357 * 2 = 5.001
 прав = +
прав = +  * 9 +
* 9 +  * 8 -
* 8 - * 5.5 +
* 5.5 +  * 2 -
* 2 -  = + 29.643 * 9 + 10 * 8 - 75 * 5.5 + 35.357 * 2 - 5 = 0
= + 29.643 * 9 + 10 * 8 - 75 * 5.5 + 35.357 * 2 - 5 = 0
 = + 29.643 * 3.64 + 10 * 2.64 - 15 * 2.64 * 1.32 = 82.03 кН*м
= + 29.643 * 3.64 + 10 * 2.64 - 15 * 2.64 * 1.32 = 82.03 кН*м
Таким образом, M max = 82.03 кН*м.
2. Обозначим опоры "A" и "B".
3. Укажем опорные реакции "
4. Составим уравнения равновесия: Σ
Σ
Σ
5. Выполним проверку, используя уравнение Y = 0:
ΣY =
ΣY = + 29.643 + 35.357 - 75 + 10 = 0.00
Ответ:
6. Стром эпюру
Эпюра
7. Стром эпюру Mx. Определеим изгибающие моменты в характерных точках:
Таким образом, M max = 82.03 кН*м.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: roman201322
Предмет: История,
автор: alinaosmakov
Предмет: Литература,
автор: zaharovn6600
Предмет: Математика,
автор: yfcnz33
Предмет: Алгебра,
автор: buuny