Предмет: Алгебра,
автор: chromium3
Запиши для функции y=f(x), где f(x)=cosx, значение: f(7π/6).
Приложения:

Ответы
Автор ответа:
4
Решение:
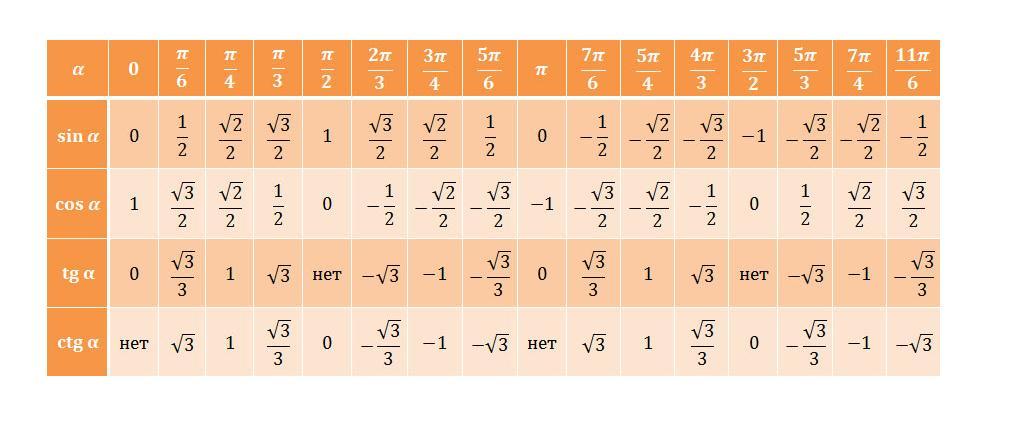
Вспомним, что , а также, что
- табличное значение. Это нам поможет решить задачу:
Ответ: 
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: Аделечка13
Предмет: Математика,
автор: RuS1234567890
Предмет: Химия,
автор: ANNAGUZ
Предмет: Алгебра,
автор: Maryashc