Question

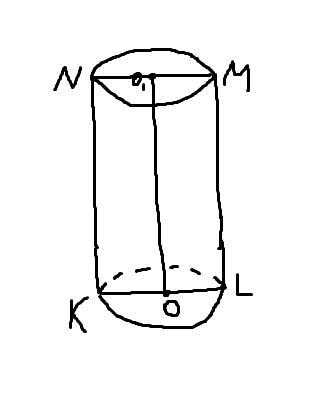
Радиус основания цилиндра относится к его высоте как 1:2. Найдите

объём цилиндра, если диагональ его осевого сечения равна 8√2

Answer 1

Ответ: $128\pi$

Пошаговое объяснение:

Осевое сечение цилиндра - это прямоугольник KLMN (диагональ KM). В прямоугольном треугольнике KLM по Теореме Пифагора: $KM^{2} =KL^{2}+ML^{2}$

Пусть радиус основания OL x, тогда LM 2x

$(8\sqrt{2}) ^2=(2x)^2+(2x)^2\\128=8x^2\\x^2=16\\x=4$

LM = 8

V = $\pi r^{2} h$ = $\pi$$*$16$*$8 = 128$\pi$