Предмет: Алгебра,
автор: Andre367541788
Помогите.
Степень с рациональным показателем
Приложения:
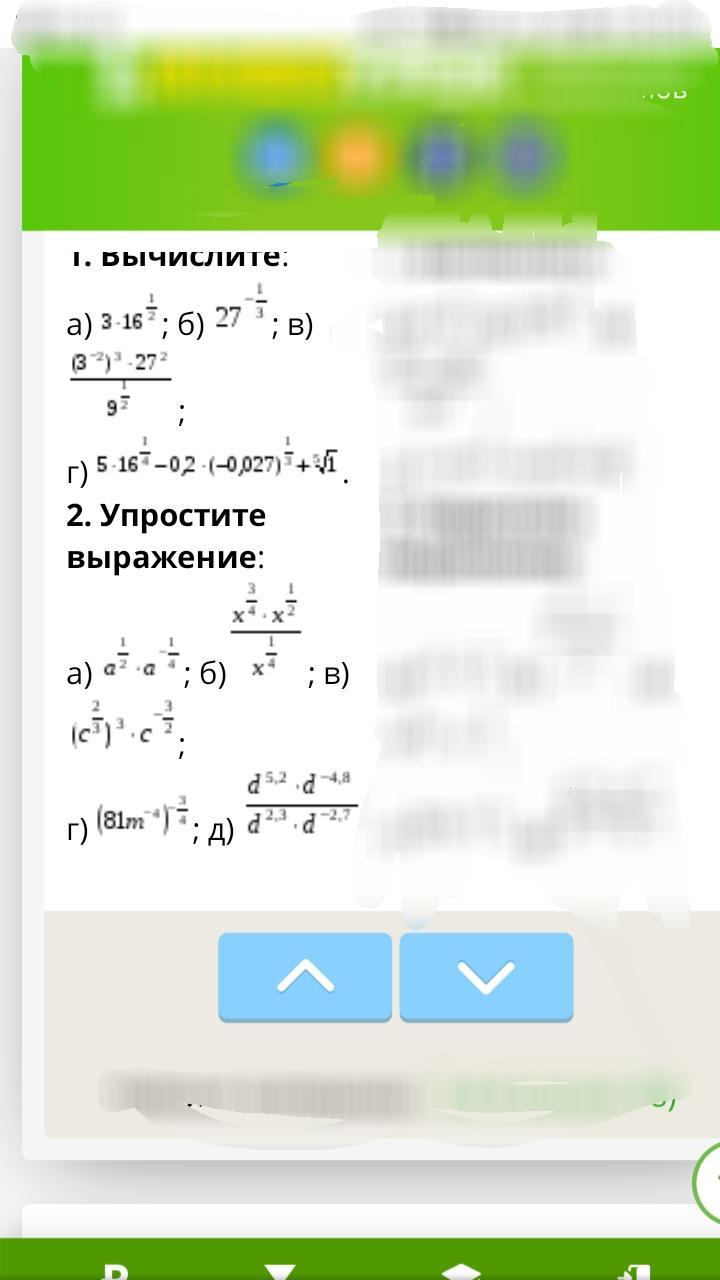
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Українська мова,
автор: kjlrf
Предмет: Українська мова,
автор: танюшка52
Предмет: Английский язык,
автор: Юлія380
Предмет: Математика,
автор: Фиона55
Предмет: Алгебра,
автор: 21127