Предмет: Геометрия,
автор: maksim69545
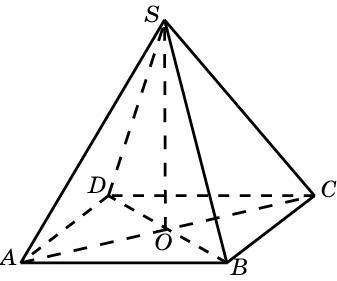
Дана правильная четырехугольная пирамида. Боковые ребра наклонены к основанию под углом 45°. Высота пирамиды равна 10 см. Найдите площадь основания пирамиды. С рисунком , заранее спасибо
Ответы
Автор ответа:
2
Ответ:
Sосн=200 см²
Объяснение:
SABCD-правильная четырехугольная пирамида⇒ABCD-квадрат, SA=SB=SC=SD
Проведём высоту SO и диагонали основания ABCD. Так как пирамида правильная четырехугольная, то AC∩BD=O
SO⊥(ABCD)⇒∠SAO=SA^(ABCD)=45°
ctg∠SAO=OA/SO⇒OA=SO·ctg∠SAO=10·ctg45°=10·1=10
ABCD-квадрат⇒OA=OC=OB=OD=0,5BD=0,5AC⇒AC=BD=2OA=2·10=20
Sосн=0,5AC·BD=0,5·20·20=200 см²
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Lexa89
Предмет: Українська мова,
автор: Mamboialoiano
Предмет: Русский язык,
автор: Yalo1
Предмет: Алгебра,
автор: Leerikaa
Предмет: Геометрия,
автор: пупс008