Question

Хорда перпендикулярна диаметру и делит его на отрезки 9 см и 4 см. Определи длину хорды.

Answer 1

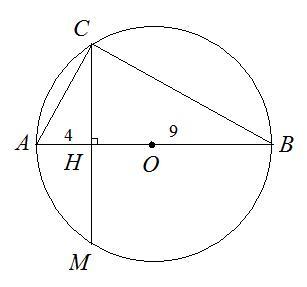
Пусть дана окружность с центорм О (см. рис.), АВ - диаметр, СМ - хорда, СМ ⊥ АМ, СМ ∩ АВ = Н, АН = 4 см, НВ = 9 см. Найдем СМ.

Соединим точки А, В и С. Получим ΔАВС - прямоугольный, т.к. ∠АСВ вписанный и опирается на диаметр, т.е. ∠АСВ = 90°. Тогда СН - высота прямоугольного треугольника, проведенная к гипотенузе, АН и ВН - проекции катетов АС и ВС на гипотенузу.

Из соотношений в прямоугольном треугольнике: высота есть среднее пропорциональное проекций катетов на гипотнузу, т.е.

СН² = АН · ВН = 4 · 9 = 36, откуда СН = 6 (см).

Т.к. Н - середина СМ (ΔАСН = ΔАМН), СМ = 2СН = 2 · 6 = 12 (см)

Ответ: 12 см.