Предмет: Геометрия, автор: Zhannaklubok

срочно нужно!!!
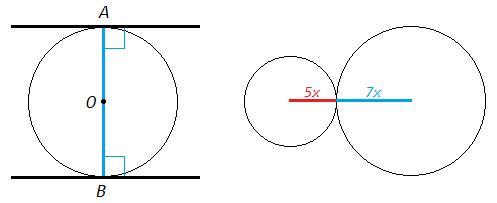
1. Две касательные к окружности параллельны.
Докажите, что расстояние между ними равно
диаметру этой окружности.

2. Две окружности касаются друг друга, а их
радиусы относятся как 5 : 7. Чему равны эти
радиусы, если расстояние между центрами
окружностей равно 36?

Zhannaklubok: во 2 задаче что дальше?

Ответы

Автор ответа: siestarjoki

1) Расстояние между параллельными прямыми - длина перпендикуляра. Проведем общий перпендикуляр AB к прямым через центр окружности O. Радиус, проведенный в точку касания, перпендикулярен касательной. Через точку можно провести только один перпендикуляр к прямой. Следовательно OA и OB - радиусы. Длина перпендикуляра AB равна двум радиусам, то есть диаметру.

2) Окружности имеют точку касания, следовательно общую касательную. Проведем радиусы в точку касания. Радиусы перпендикулярны касательной и составляют развернутый угол. Точка касания лежит на линии центров. Расстояние между центрами равно сумме радиусов.

R1=5x, R2=7x

R1+R2 =12x =36 => x=3

R1=15, R2=21

Приложения:

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Қазақ тiлi, автор: 9ВикториЯ9

Жақсылық Үшкемпіров - еркін күрестен Қазақстан чемпионы, грек-рим күресінен КСРО-ның екі дүркін чемпионы, әлем чемпионаты мен кубогының жеңімпазы, КСРО-ның еңбек сіңірген спорт шебері. ол 1980 жылғы Мәскеу Олимпиадасында қарсыластарының бәрін жеңіп,Қазақстаннан шыққан тұңғыш Олимпиада чемпионы атанды. 1984 жылы Красноярск қаласында жалауын көтерген КСРО кубогында 33 жастағы Жақсылық Үшкемпіровті үлкен спорттан шығарып салу рәсімі жоғары деңгейде ұйымдастырылды...переведите пжл на русский язык!СРОЧНО!!!

1 год назад

Предмет: Английский язык, автор: dorzhiklimon

Checks and Balances The Constitution provides for three main branches of government which are separate and distinct from one another. The powers given to each are carefully balanced by the powers of the other two. Each branch serves as a check on the others. This is to keep any branch from gaining too much power or from misusing its powers. The chart 20 below illustrates how the equal branches of government are connected and how each is dependent on the other two. Congress has the power to make laws, but the President may veto any act of Congress. Congress, in its turn, can override a veto by a two-thirds vote in each house. Congress can also refuse to provide funds requested by the President. The President can appoint important officials of his administration, but they must be approved by the Senate. The President also has the power to name all federal judges; they, too, must be approved by the Senate. The courts have the power to determine the constitutionality of all acts of Congress and of presidential actions, and to strike down those they find unconstitutional. The system of checks and balances makes compromise and consensus necessary. Compromise is also a vital aspect of other levels of government in the United States. This system protects against extremes. It means, for example, that new presidents cannot radically change governmental policies just as they wish. In the U.S., therefore, when people think of "the government," they usually mean the entire system, that is, the Executive Branch and the President, Congress, and the courts. In fact and in practice, therefore, the President (i.e. "the Administration") is not as powerful as many people outside the U.S. seem to think he is. In comparison with other leaders in systems where the majority party forms "the government," he is much less so.

1 год назад

Предмет: Русский язык, автор: den4ик

сочинение-рассуждение ,,зачем нужно читать,,

1 год назад

Предмет: Математика, автор: Аноним

Дан лист клетчатой бумаги 4*4. Соедините вершины некоторых квадратиков так, чтобы получился четырех угольник , площадь которого была бы в 10 раз больше площади одного квадратика

8 лет назад

Предмет: Математика, автор: 23Илья32

В гостинице 1000 номеров и они нумеруются подряд, начиная с 1. На дверях каждого висит табличка с указанием номера. Сколько раз на этих табличках встречается цифра 3?

8 лет назад