Предмет: Алгебра,
автор: Sidorovich
Найти производную определенного интеграла
Приложения:
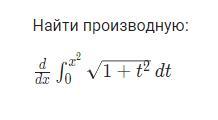
Ответы
Автор ответа:
0
Нужно вычислить
F(0) - конечное число, а тогда
По теореме о дифференцировании композиции функций имеем
Похожие вопросы
Предмет: Українська мова,
автор: natysi2002
Предмет: Английский язык,
автор: timur007007
Предмет: Русский язык,
автор: masha131313
Предмет: Математика,
автор: anyamedvedeva4
Предмет: Математика,
автор: casicka