Предмет: Геометрия,
автор: dasatotackaa
Помогите!!! Пожалуйста!!!!!!!!!!!
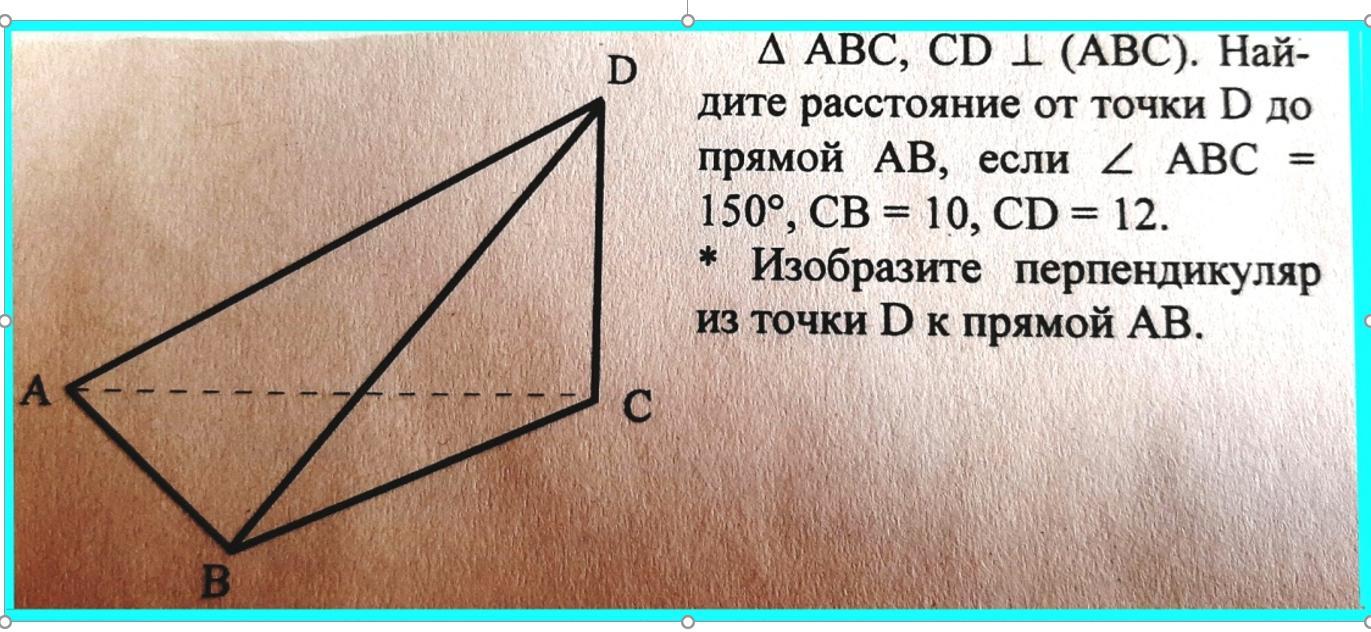
Треугольник АВС, СD ⊥ АВС. Найдите расстояние от точки D...
Приложения:
Ответы
Автор ответа:
0
Ответ:
13
Объяснение:
DC⊥(ABC), ∠ABC=150°, CB=10, CD=12
DC⊥(ABC), BC∈(ABC)⇒DC⊥BC
Опустим из точки С перпендикуляр на прямую АВ. Очевидно, то что основание этого перпендикуляра Е будет принадлежать не отрезку АВ , а его продолжению за точку В. Это из-за того что ∠ABC=150°-тупой.
∠СВЕ=180°-∠ABC=180°-150°=30°, ∠СЕВ=90°⇒СЕ=0,5ВС=0,5·10=5
∠DСЕ=90°⇒DЕ²=СЕ²+DС²=5²+12²=169⇒DЕ=13
DC⊥(ABC), Е∈(ABC)⇒отрезок СЕ- орт.проекция отрезка DЕ
CЕ⊥АB⇒DЕ⊥АВ⇒DЕ-отрезок определяющий расстояние от точки D до прямой АВ.
Достоверность требуемого построения доказана по ходу решения задачи.
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: Vessy
Предмет: Українська мова,
автор: unguryan2014
Предмет: История,
автор: irinakomedina12
Предмет: История,
автор: Аноним