Предмет: Алгебра,
автор: angelalizogub
Знайдіть корені квадратного рівняння
(3x-1)(х+3)=x(1+6x)
Допоможіть
Ответы
Автор ответа:
1
оберіть розв'язок як кращу відповідь, будь ласка
Приложения:
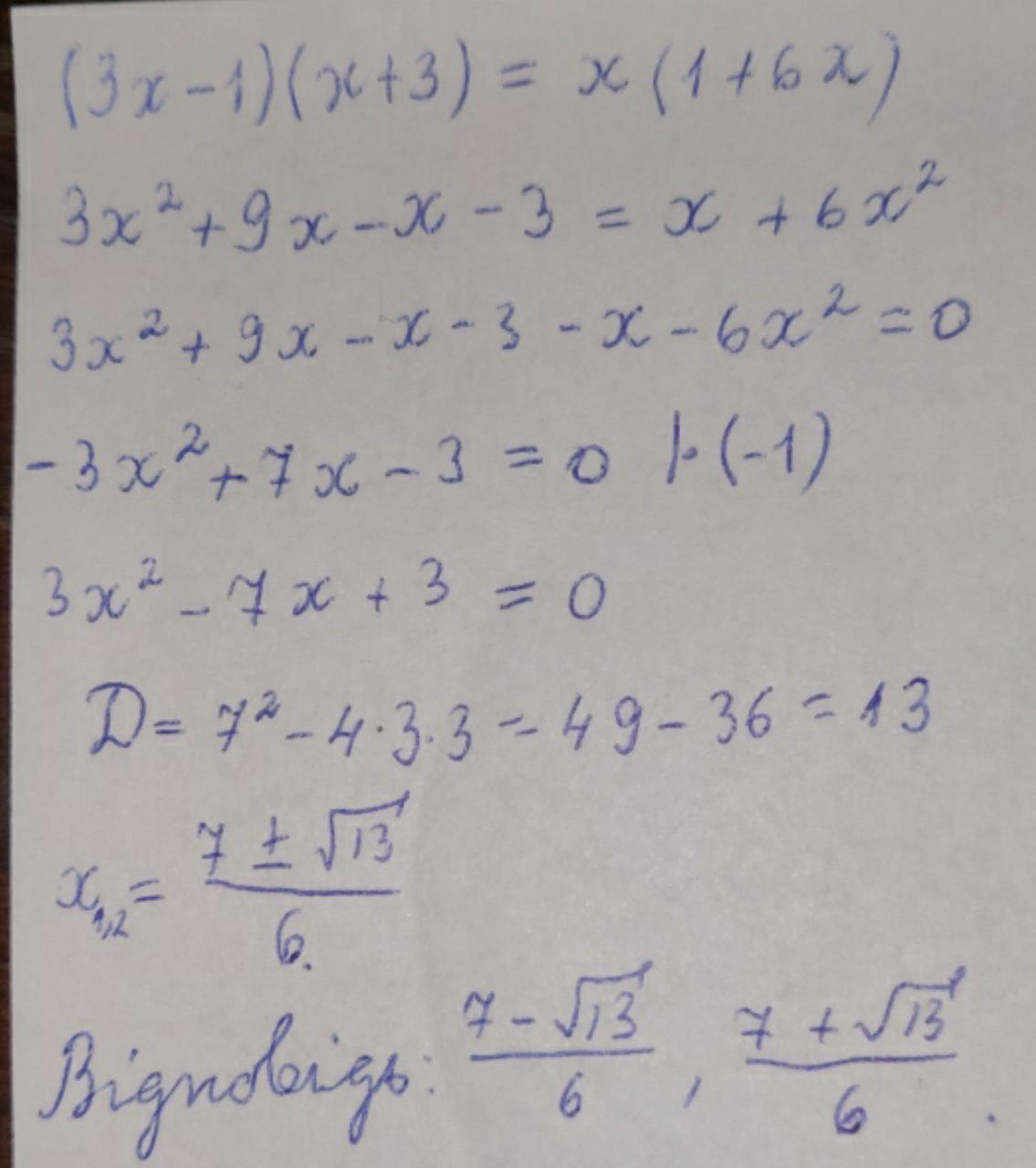
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: rustam17111999
Предмет: Английский язык,
автор: AlexOcean
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: qasimovanermin
Предмет: Математика,
автор: verbatanyalovey