Предмет: Алгебра,
автор: Volf213
Пожалуйста помогите!!! С решением
Приложения:
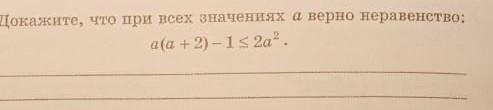
Ответы
Автор ответа:
1
Ответ:
вот готово
Объяснение:
Приложения:

oganesbagoyan:
≥ 0
Автор ответа:
1
Так как последнее неравенство выполняется при любых значениях "а" , то значит выполняются и все неравенства, записанные выше, при любых значениях "а" , значит доказано, что при всех значениях "а" .
Похожие вопросы
Предмет: Английский язык,
автор: Demonessа
Предмет: Английский язык,
автор: sergey2002
Предмет: Русский язык,
автор: YulyK
Предмет: Геометрия,
автор: Kiba2017
Предмет: Математика,
автор: Ann48r