Question

Найдите, при каких значениях числа a, система уравнений x^2+y^2=9; x+y=a, имеет два решения.​

Answer 1

Имеем систему уравнений:

$\displaystyle \left \{ {{x^{2} + y^{2}=9} \atop {x +y = a \ \ \ }} \right.$

где $x^{2} + y^{2} = 3^{2}$ — уравнение окружности с центром $(0; \ 0)$ и радиусом $3$, $x + y = a$ — прямая, проходящая через $\text{II}$ и $\text{IV}$ координатные четверти под углом $45^{\circ}$ вдоль положительного направления оси абсцисс.

Система имеет три варианта решения:

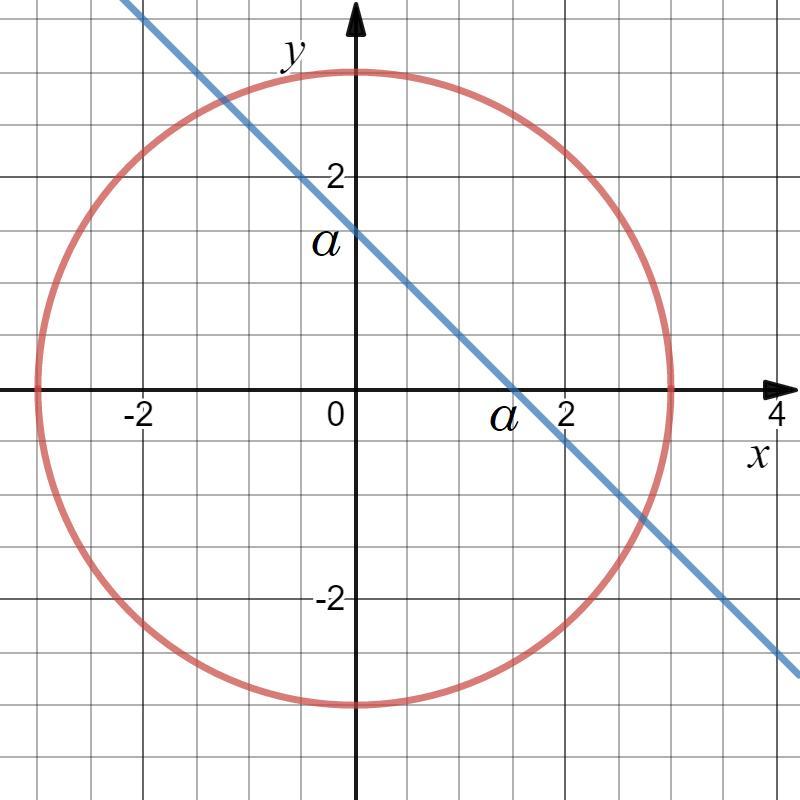
1) иметь два решения (см. вложение);

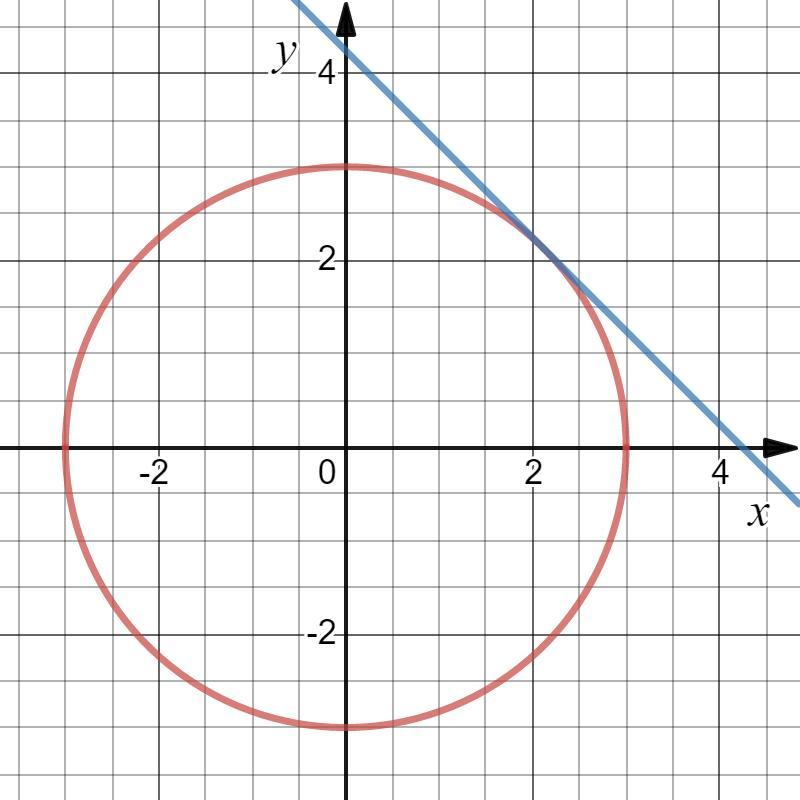
2) иметь одно решение (см. вложение);

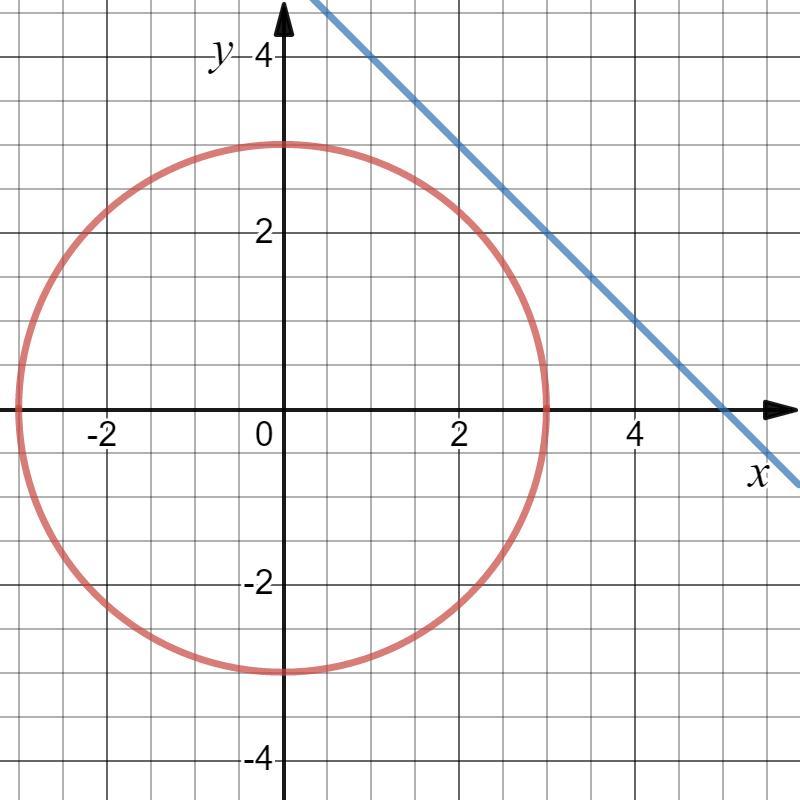
3) не иметь решений (см. вложение);

Нам подойдет первый вариант. Решим данную систему уравнений методом подстановки.

$\displaystyle \left \{ {{x^{2} + y^{2}=9} \atop {x = a - y \ \ \ }} \right.$

$(a - y)^{2} + y^{2} = 9\\a^{2} - 2ay + y^{2} + y^{2} = 9\\2y^{2} - 2ay + a^{2} - 9 = 0$

$D = (-2a)^{2} - 4 \cdot 2 \cdot (a^{2} - 9) = 4a^{2} - 8a^{2} + 72 = 72 - 4a^{2}$

Данное уравнение будет иметь два корня, если $D>0$, то есть если $72 - 4a^{2} > 0$

$4a^{2} < 72\\a^{2} < 18$

$a^{2} = 18$

$a = \pm3\sqrt{2}$

$a \in (-3\sqrt{2}; \ 3\sqrt{2})$

Именно при таких значениях параметра $a$ данная система уравнений будет иметь два решения.

Ответ: $a \in (-3\sqrt{2}; \ 3\sqrt{2})$