ХЭЛП! 30 БАЛЛОВ! Для тех, кто разбирается в математике.
Уравнение внизу, на картинке.
В этом уравнении ведь ОДЗ будет х ≠ -1.
Вопрос: когда мы пишем ОДЗ и указываем при каких значениях знаменатель равен нулю ( в моём случае это -1), то ЗНАМЕНАТЕЛЬ АВТОМАТИЧЕСКИ ПРОПАДАЕТ, или мне нужно его убрать (т.е. умножить уравнение на х+1)?
Очень важный для меня вопрос, и за ответ буду очень благодарна).
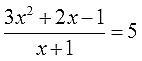
Ответы
Ответ: x=2.
Объяснение:
(3x²+2x-1)/(x+1)=5 ОДЗ: x+1≠0 x≠-1 ⇒ x∈(-∞;-1)U(-1;+∞).
(3x²+2x-1)/(x+1)=5 |×(x+1)
3x²+2x-1=5*(x+1)
3x²+2x-1=5x+5
3x²-3x-6=0 |÷3
x²-x-2=0 D=9 √D=3
x₁=2 ∈ОДЗ x₂=-1 ∉ОДЗ
Ответ: х=2.
Предлагаю для начала решить уравнение:
(3x² + 2x - 1)/(x + 1) = 5
ОДЗ: x + 1 ≠ 0
x ≠ -1
(3x² + 2x - 1)/(x + 1) * (x + 1) = 5 * (x + 1)
3x² + 2x - 1 = 5 * (x + 1)
3x² + 2x - 1 = 5x + 5
3x² + 2x - 5x - 1 - 5 = 0
3x² - 3x - 6 = 0
D = (-3)² - 4 * 3 * (-6) = 9 + 72 = 81
x₁,₂ = (3 ± √81)/(2 * 3) = (3 ± 9)/6
x₁ = (3 + 9)/6 = 12/6 = 2
x₂ = (3-9)/6 = -6/6 = -1 (посторонний корень, не соответствует ОДЗ).
ОТВЕТ: x = 2.
Отвечаю на Ваш вопрос.
В дробно-рациональных уравнениях (подобных данному) нужно избавляться от знаменателя. Он никуда автоматически не пропадает. Просто все уравнение имеют такую особенность, что если умножить обе чести уравнения на одно и то же число (или выражение), то корни уравнения остаются прежними. В таком случае чтобы "исчез" знаменатель (то есть чтобы от него избавиться) обе части уравнения умножают на общий знаменатель (вторая строчка решения, не учитывая ОДЗ).