Question

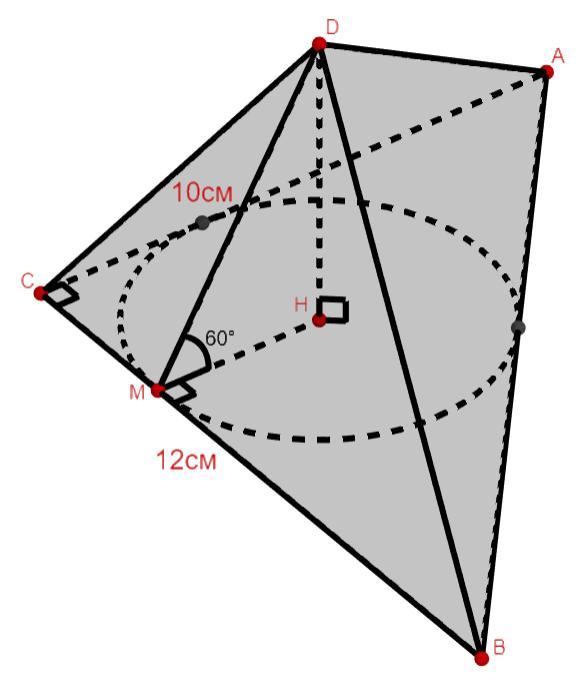
В основании пирамиды –прямоугольный треугольник, катеты которого равны 10 см и 12 см; все боковые грани пирамиды наклонены к основанию под углом 60 0 . Найдите высоту пирамиды.

Answer 1

Если боковые грани пирамиды равнонаклонены к плоскости основания, то главная высота пирамиды падает в центр вписанной, в основание, окружности.

В прямоугольном ΔABC (∠C=90°) найдём гипотенузу, по теореме Пифагора. AB=√(10²+12²)=2√(25+36)=2√61 см

Радиус вписанной окружности HM=(AC+BC-AB)/2

HM=(10+12+2√61)/2 = 11+√61 см

В прямоугольном ΔDHM (∠H=90°):

$tg(\angle DMH)=\dfrac{DH}{MH}$

Откуда DH = MH·tg(∠DMH) = (11+√61)·tg60° = √3·(11+√61) см

Ответ: 11√3+√183 см.