Question

Решите 2 задачи пожалуйста!!!!

Answer 1

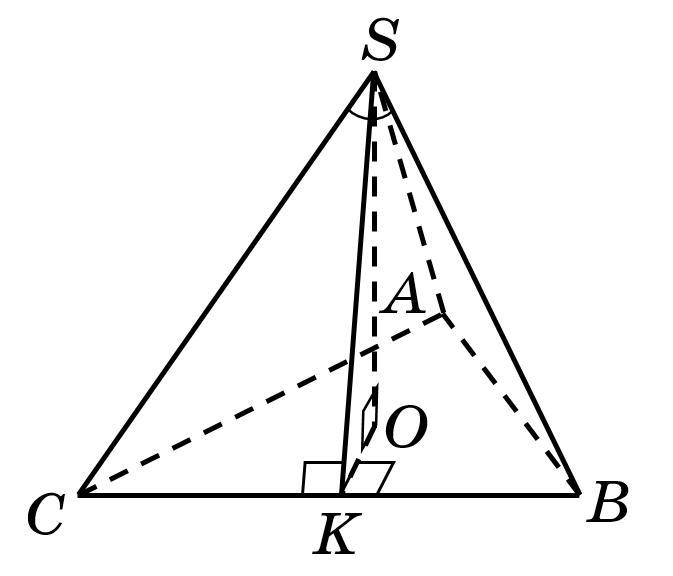
1) Пусть дана правильная пирамида $SABC$, основанием которой является правильный треугольник $ABC$ со стороной $BC = 8$, угол $CSB = 60^{\circ}$ (см. вложение).

$SO$ — высота пирамиды $SABC$.

Рассмотрим треугольник $BSC$: так как пирамида правильная, то $\angle B = \angle C$ которые равны $180 - 2 \cdot 60 = 60^{\circ}$. Следовательно, треугольник

Рассмотрим прямоугольный треугольник $SKB (\angle K = 90^{\circ}):$

$SK = BK \cdot \text{ctg} \, 30^{\circ} = 4 \sqrt{3}$

Пусть $OK$ — проекция $SK$ на плоскость $(ABC)$. Тогда по теореме о трех перпендикулярах $OK \perp BC$. Здесь

Таким образом, $OK = \dfrac{BC}{2\sqrt{3}} = \dfrac{8}{2\sqrt{3}} = \dfrac{4\sqrt{3}}{3}$

Рассмотрим прямоугольный треугольник $SOK (\angle O = 90^{\circ})$

$SO = \sqrt{SK^{2} - OK^{2}} = \sqrt{(4\sqrt{3})^{2} - \left(\dfrac{4\sqrt{3}}{3} \right)^{2}} = \sqrt{48 - \dfrac{48}{9}} = \sqrt{\dfrac{384}{9} } =\dfrac{8\sqrt{6}}{3}$

Ответ: $\dfrac{8\sqrt{6}}{3}$

Примечание. В задаче не указано, что пирамида правильная, но только при таком условии мы можем решить исходную задачу, иначе расположение вершины $S$ пирамиды может быть различным и, следовательно, ответ может быть различным.

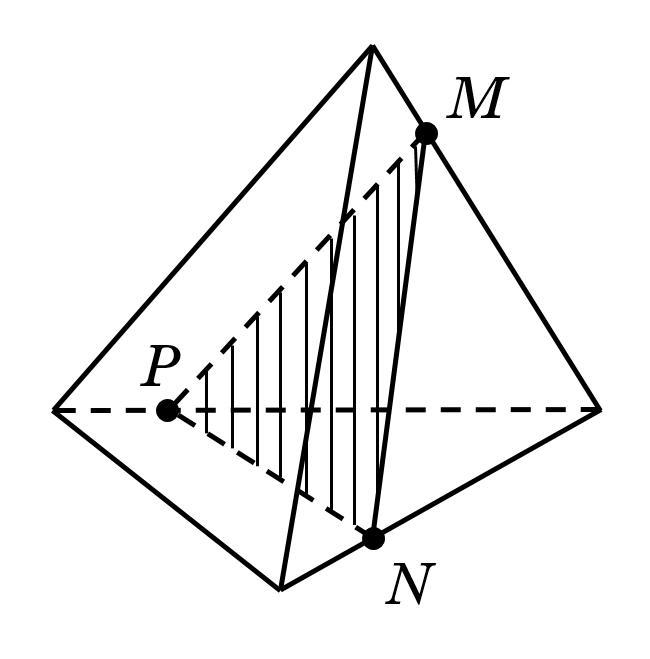
2) Самое главное правило при построение сечений: соединять можно две точки, лежащие в одной плоскости. И следует помнить, что прямые в пространстве бесконечны, поэтому их можно продлевать и искать новые точки.

Точки $M$ и $N$ можно соединить, поскольку они обе лежат в одной грани, точно также можно соединить точки