Помогите пожалуйста, у меня тест!!!
2)
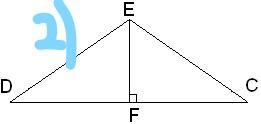
EC=ED,∢DEC=113°.
Угол FDE равен ...
3)
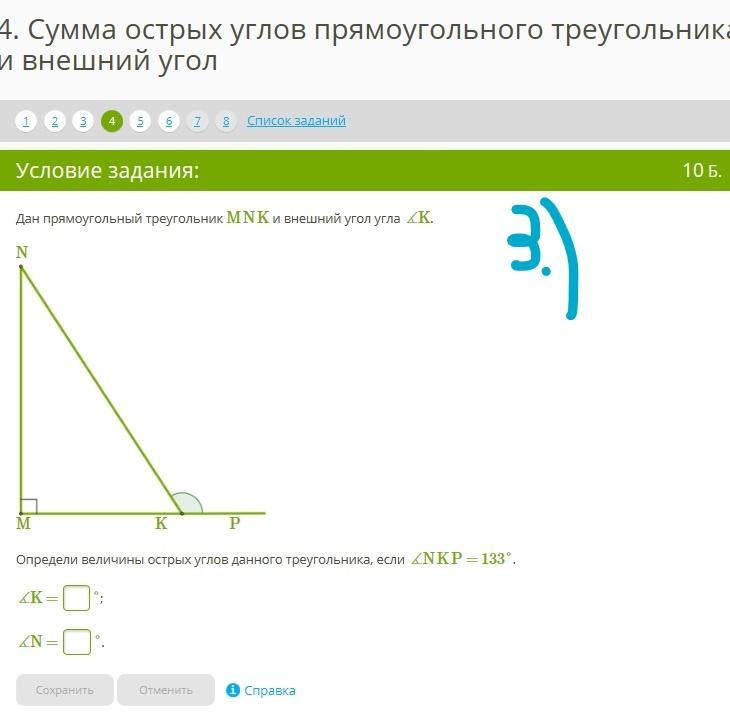
Дан прямоугольный треугольник MNK и внешний угол угла ∡K
Определи величины острых углов данного треугольника, если ∡NKP=133°
∡K=...°;
∡N=...°.
4)
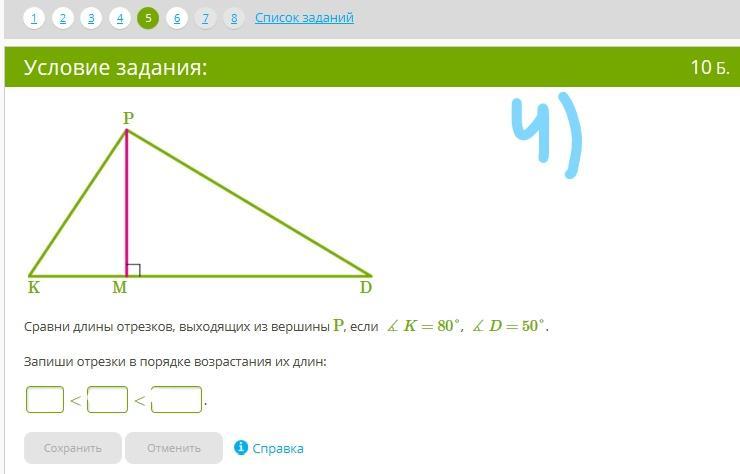
Сравни длины отрезков, выходящих из вершины P, если ∡K=80°, ∡D=50°.
Запиши отрезки в порядке возрастания их длин:
... < ... < ...
5)
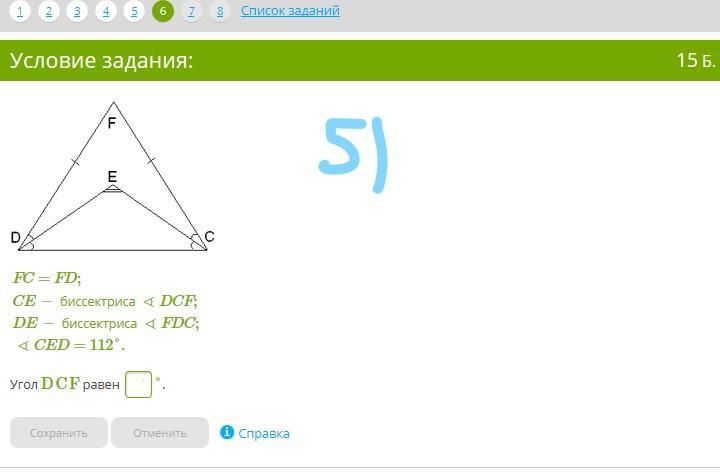
FC=FD;
CE− биссектриса∢DCF;
DE− биссектриса∢FDC;
∢CED=112°.
Угол DCF равен ... °.
6)
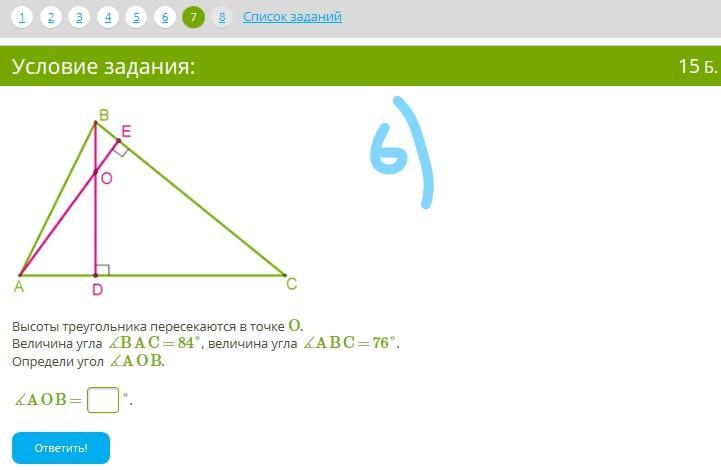
Высоты треугольника пересекаются в точке O.
Величина угла ∡BAC=84°, величина угла ∡ABC=76°.
Определи угол ∡AOB.
∡AOB=°.
Ответы
Ответ:
Объяснение:
2) Треугольник, по-видимому, равнобедренный?
Если так, то углы D и С равны. Сумма всех углов в треугольнике = 180°.
Если ∢DEC=113°, то сумма углов D+C = 180° - 113° = 67°.
Каждый из углов при основании равен: 67° / 2 = 33,5°
3) Углы NKP и NKM - смежные и в сумме равны 180°
Угол NKM: 180° - 133° = 47°
Сумма всех углов в треугольнике = 180°
Угол NMK = 90° как прямой угол
Угол MNK: 180° - 47° - 90° = 43°
Величины острых углов: MNK - 43°, NKM - 47°
4)Отрезки, проведённые из вершины треугольника к его основанию, тем короче, чем больше угол между данным отрезком и основанием треугольника. И соответственно чем угол меньше, тем отрезок длиннее.
1) Угол К (=80˚) между боковой линией РК и основанием KD по величине больше , чем угол D (=50˚) между боковой линией РD и основанием KD. Поэтому сторона РК при угле К короче, чем сторона РD при угле D: PK<PD
2) Поскольку отрезок РМ проведён к основанию под углом 90˚, то он является высотой треугольника. А высота – это самый короткий отрезок, проведённый из вершины треугольника к его основанию.
Тогда: PM<PK<PD
(5)
1) Поскольку FC=FD, то треугольник DFC равнобедренный. Треугольник DЕC также равнобедренный, поскольку Е - точка пересечения равных биссектрис из равных углов при основании равнобедренного треугольника.
Поскольку треугольник DFC равнобедренный, то углы при основании равны:
∢ЕDC=∢ЕCD
Тогда, согласно теореме про сумму углов треугольника:
∢ЕDC+∢ЕCD+∢DЕC = 180°,
Значит, ∢ЕDC=∢ЕCD = (180° - ∢DЕC) / 2 = (180° - 112°) / 2 = 68° / 2 = 34°
2) Биссектрисы СЕ и DЕ делят углы, из которых они проведены пополам,
поэтому: ∢FЕC и ∢FDC больше углов ∢ЕDC и ∢ЕCD в два раза:
∢CDF = ∢ЕDC х 2 = 68 х 2 = 136°
∢DCF = ∢ЕCD х 2 = 68 х 2 = 136°
(6)
Все углы находим согласно теореме про сумму углов треугольника: А + В + С = 180°
1) ∢ВАС+∢АВС+∢АСВ = 180°
Находим ∢АСВ: 180° - (∢ВАС+∢АВС) = 180 - 84 – 76 = 20°
2) ∢ВDС = 90°, ∢DСВ=∢АСВ; ∢DВС = 180° - (∢ВDС + ∢DСВ) = 180 – (90 + 20) = 70°
3) ∢AEB = 90°, ∢BOE = 180° - (∢AEB + ∢DСВ) = 180 – (90 + 70) = 20°
4) Углы ∢BOE и ∢AОB – смежные и в сумме составляют 180°
Тогда: ∢AОB = 180° - ∢BOE = 180° - 20° = 160°
Ответ: ∢AОB = 160°