Решите неравенство ( объясните решение)
(x-3)^2x^2-7x>1
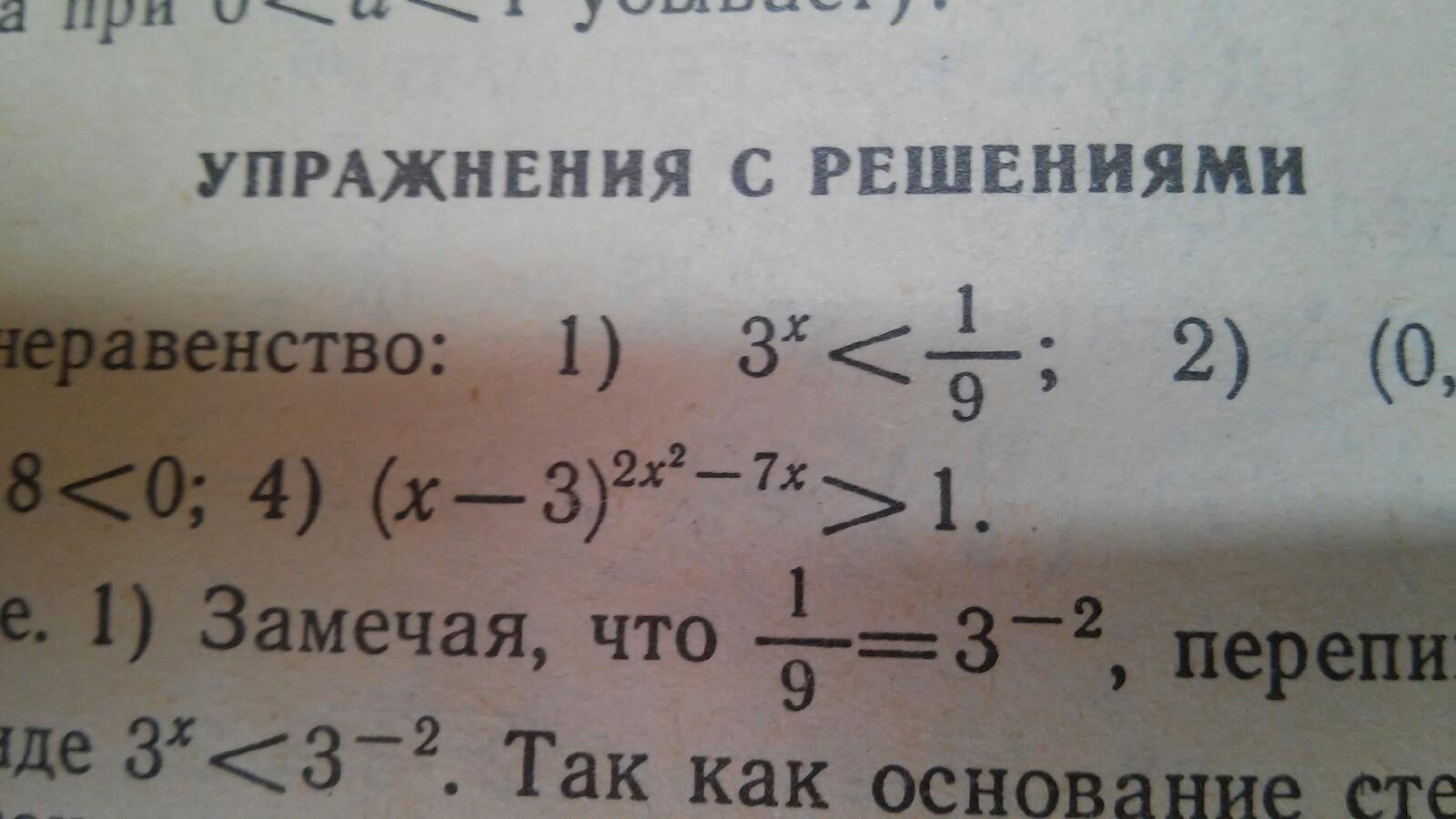
Ответы
ОДЗ: при
— любое, и
, если
.
Прологарифмируем обе части неравенства с основанием, например, 3.
По свойству логарифма имеем:
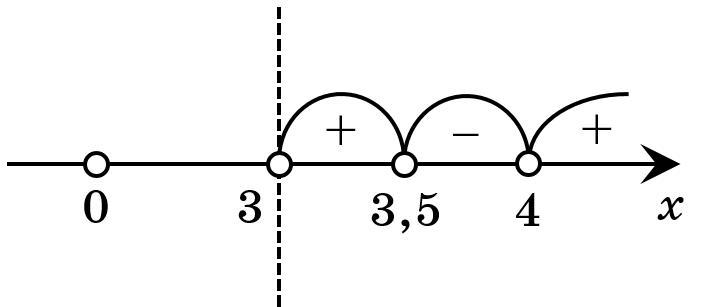
Решим неравенство методом интервалов (обобщенный).
1) Найдем ОДЗ:
2) Найдем значения , при которых функция
равна нулю (найдем нули функции):
Произведение множителей равно нулю, когда хотя бы один из них равен нулю:
не удовлетворяет ОДЗ.
3) Разобьем область определения на промежутки, каждый из концов которого является корнем уравнения или конечной точкой промежутка определения функции
4) Определим знак на каждом из образовавшихся промежутков.
5) Объединим промежутки, на которых функция удовлетворяет неравенству, во множество решений.
Смотрите вложение.
Получаем решение:
Разберем случай, когда при
(поскольку отрицательное число можно возводить только в целую степень). Пусть
где
. Тогда
Здесь при
Так как , то
При получается неопределенность
в исходном неравенстве.
Если при
, то данное неравенство будет выполнятся в таких случаях:
1) если основание степени , то есть если
, то показатель степени равен:
Значит, при имеем:
2) если основание степени , то есть если
, то показатель степени должен быть четным и целым положительным, то есть
, поскольку если в основании степени находится число, меньшее
, то сама степень может быть больше единицы тогда и только тогда, когда показатель степени — четное натуральное число, поэтому выполняется только
где
.
Ответ: