Предмет: Математика,
автор: nooneB
Решить дифференциальное уравнение и определить тип
Приложения:
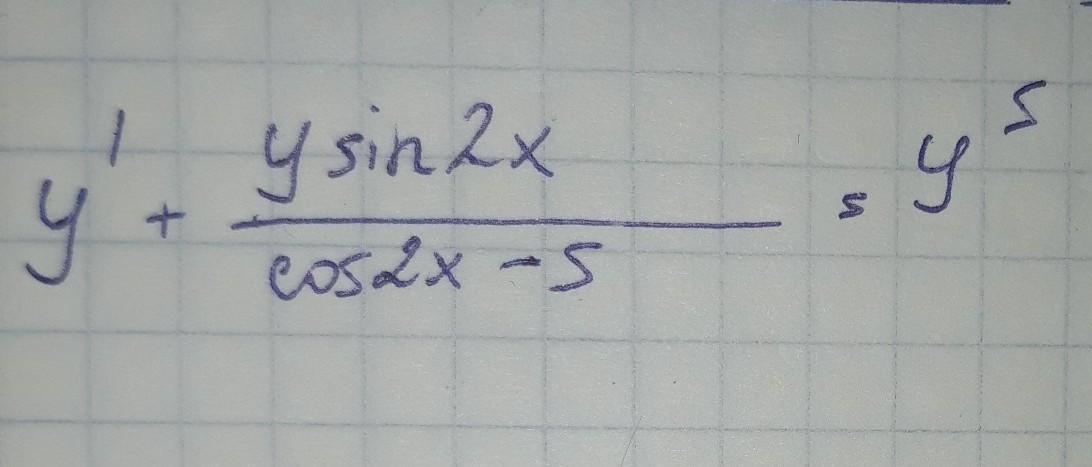
Аноним:
Справа y в пятой степени?
да
Уравнение Бернулли
через уравнение Бернулли решать?
Это ОДУ Бернулли.
Ответы
Автор ответа:
2
Тип: линейное неоднородное дифференциальное уравнение первого порядка.
Поделим обе части уравнения на , получим
Пусть , тогда
, получаем
Далее умножим обе части последнего уравнения на
Похожие вопросы
Предмет: Другие предметы,
автор: lilia2127
Предмет: Другие предметы,
автор: timva
Предмет: Английский язык,
автор: Денисссс
Предмет: Математика,
автор: няшка285