Предмет: Алгебра,
автор: darkomarco
Логарифмическое неравенство 9 (1/5 заменить на 1/2, там неправильно иначе)
Приложения:
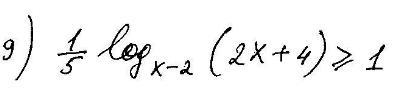
Ответы
Автор ответа:
1
Ответ: x∈(3;6].
Объяснение:
(1/2)*logₓ₋₂(2x+4)≥1 |×2
logₓ₋₂(2x+4)≥2
ОДЗ: x-2>0 x>2 x-2≠1 x≠3 2x+4>0 2x>-4 |÷2 x>-2 ⇒
x∈(2;3)U(3;+∞).
1) x∈(2;3)
2x+4≤(x-2)²
2x+4≤x²-4x+4
x²-6x≥0
x*(x-6)≥0
-∞__+__0__-__6__+__+∞
x∈(-∞;0]U[6;+∞) ⇒ x∉
2) x∈(3;+∞)
2x+4≥(x-2)²
2x+4≥x²-4x+4
x²-6x≤0
x*(x-6)≤0
-∞__+__0__-__6__+__+∞
x∈[0;6] ⇒
x∈(3;6].
Аноним:
Здравствуйте можете мне помочь с математикой пожалуйста умоляю
Давайте задание.
сейчас
https://znanija.com/task/34516039?utm_source=android&utm_medium=share&utm_campaign=question
№330 и №331?
https://znanija.com/task/34516039? не открывается.
Автор ответа:
1
ОДЗ:
х-2 >0 x>2
x-2≠1 x≠3
при х-2 > 1
x ∈[0;6] x-2 > 1 => x∈(3;6]
при 0< х-2 < 1
при 2<x<3
учитывая, что 2<x<3 то в данном случае ∅
Ответ: x∈(3;6]
Похожие вопросы
Предмет: Русский язык,
автор: karunina
Предмет: Русский язык,
автор: Аноним
Предмет: Другие предметы,
автор: olesy1985
Предмет: Информатика,
автор: Katiksokolova
Предмет: Химия,
автор: teemant