Предмет: Алгебра,
автор: ffugglyy
помогите!!! пожалуйста!!! 11 класс алгебра
Приложения:
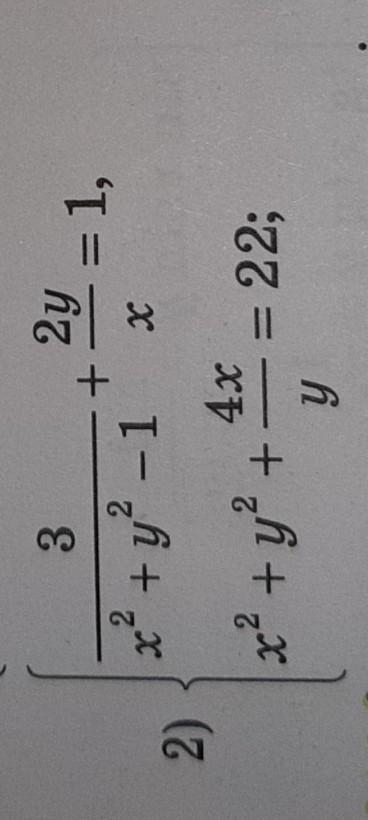
Ответы
Автор ответа:
1
Автор ответа:
1
Ответ: во вложении Объяснение:
Приложения:

Похожие вопросы
Предмет: Другие предметы,
автор: SunnyBlondy
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: 7778598
Предмет: Алгебра,
автор: nika2016kim
Предмет: Математика,
автор: alva09