Предмет: Алгебра,
автор: Сайдет
Решите пж!!! СРОЧНОООО!!!!!
Приложения:
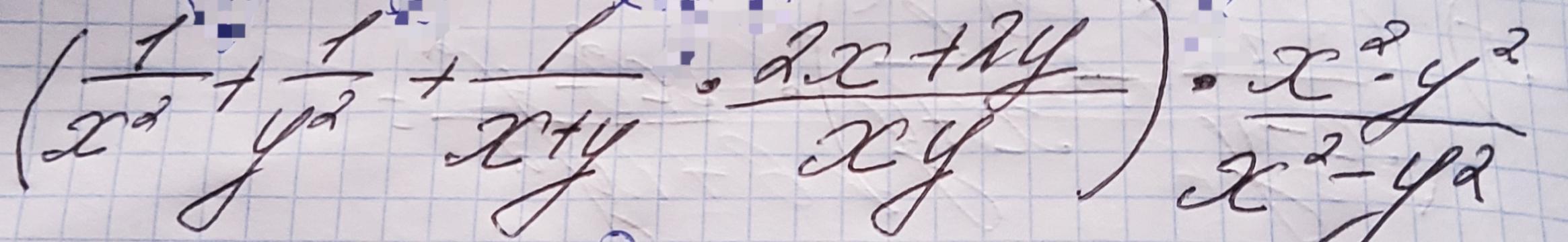
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Українська мова,
автор: 131404060
Предмет: Английский язык,
автор: МаЛеНьКаЯ28
Предмет: Українська мова,
автор: Alinka287
Предмет: Алгебра,
автор: иришка98