Предмет: Алгебра,
автор: kostruleva1985
Помогите пожалуйста решить номер 142(1 и2 примеры). Заранее благодарю
Приложения:
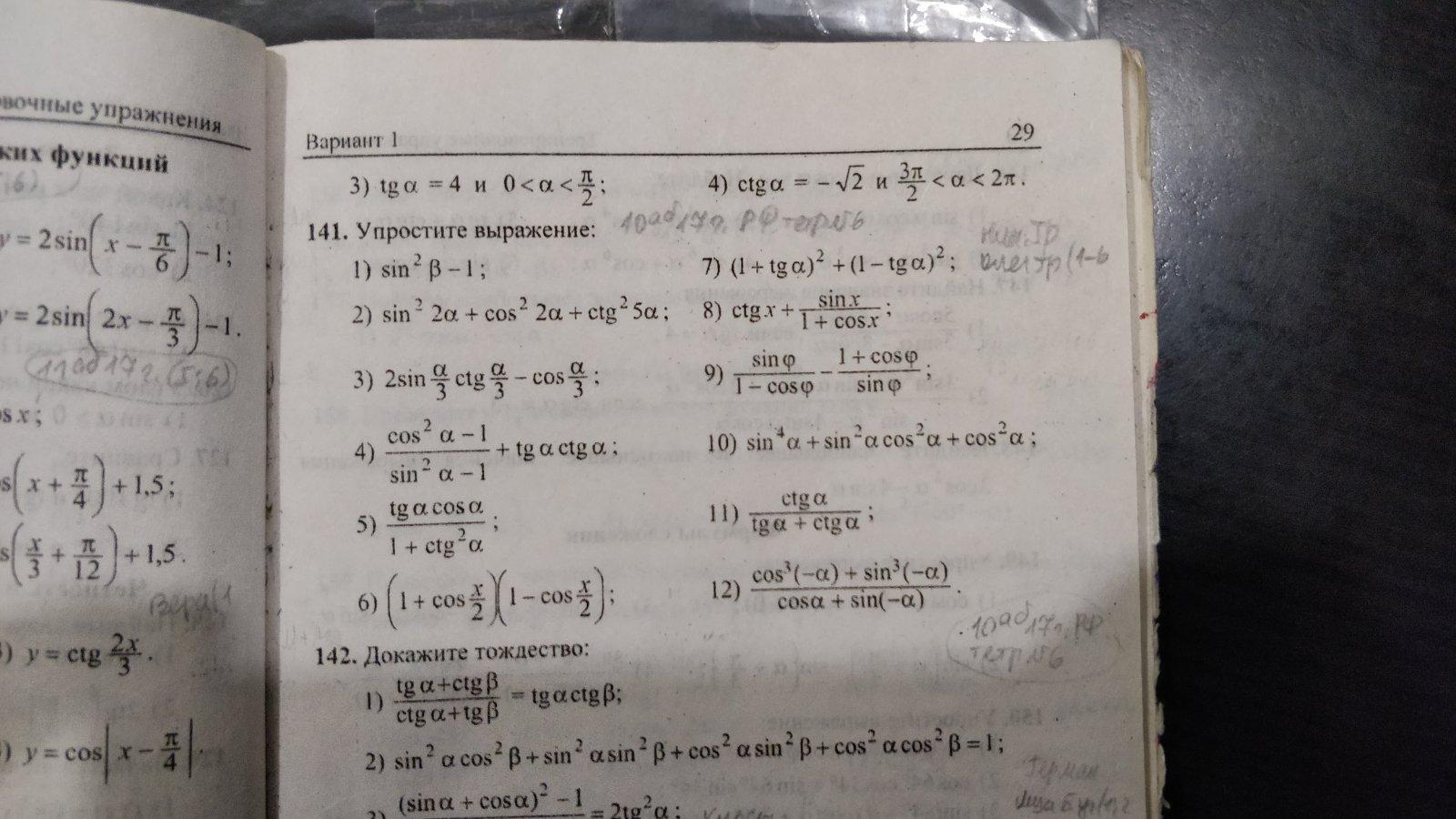
Ответы
Автор ответа:
3
1)
2)
Автор ответа:
1
Ответ: во вложении Объяснение:
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: кристинка190199
Предмет: Русский язык,
автор: Леонид1549
Предмет: Қазақ тiлi,
автор: Aleksandr999
Предмет: Математика,
автор: natashach2000