Предмет: Алгебра,
автор: Jamba00
Помогите пожалуйста
Тригонометрия
Приложения:
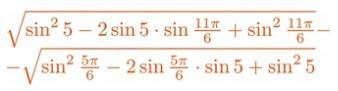
Аноним:
эх ты
Ответы
Автор ответа:
2
Ответ:
-1
Объяснение:
Под радикалами используем формулу квадрата разности
Пользуемся формулой:
При раскрытии модуля учитываем, что
Спасибо большое!
Подождите, я ошибку нашла. Сейчас исправлю.
Исправила.
)))
Ну слушайте. Нужно доказать, что sin5 + 1/2 < 0.
Автор ответа:
1
Ответ: во вложении Объяснение:
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: viktoria200210
Предмет: Русский язык,
автор: volleyballcoldplay
Предмет: Русский язык,
автор: коля166666
Предмет: История,
автор: Nastya08121