Предмет: Алгебра,
автор: Qoqoqoqoqp
Помогите найти границу
Приложения:
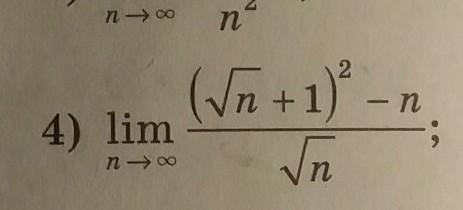
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: volleyballcoldplay
Предмет: Русский язык,
автор: коля166666
Предмет: Русский язык,
автор: МНекрасова
Предмет: Математика,
автор: ПеЧеНьКаСшОкАм