Предмет: Алгебра,
автор: ustlera
11 класс. Уравнение с параметром. Ответ — [2,5; 3,5], у меня не сходится (получается [2,8; 6]).
Приложения:
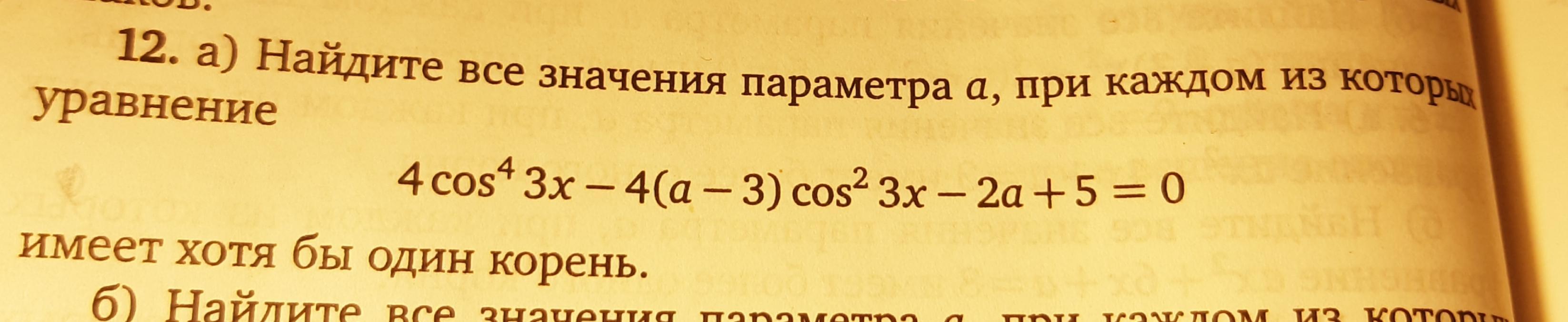
Ответы
Автор ответа:
2
рассмотрим наше уравнение:
выполним замену cos²3x=t; t≥0
чтобы уравнение имело хотя бы один корень надо чтобы D≥0
Это неравенство выполняется для любых a
тогда проверим корни, необходимо чтобы t≥0
рассмотрим первый корень
значит при а≥2.5 мы получим один положительный корень (относительно t)
проверим второй корень
тут положительных корней не получим.
значит рассмотрим один положительный корень t=(2a-5)/2. при а≥2,5
выполним обратную замену
рассмотрим положительный корень
рассмотрим отрицательный корень
выполняется для всех а≥2.5
Собираем все вместе 2,5≤а≤3,5
ustlera:
Огромное спасибо! А что означают условия "1.1a>=2", "2.1>=2" и пр.?
Это раскрытие модуля
Еще раз спасибо. Так, это мой первый вопрос, поэтому я не знаю, что к чему. Баллы за ответ отправляются автоматически, или я должна отправить их как-то сама?
все происходит автоматически)
лучший ответ вам предложат поставить
и человеку ответившему будет приятно и вы обратно часть баллов получите
и человеку ответившему будет приятно и вы обратно часть баллов получите
пока не вижу такой кнопки, может, позже появится
Похожие вопросы
Предмет: Русский язык,
автор: Vovakom
Предмет: Английский язык,
автор: swoker
Предмет: Русский язык,
автор: Delet15
Предмет: Математика,
автор: OlesyaLisina
Предмет: Алгебра,
автор: mmsrhz