Помогите, пожалуйста с алгеброй!
Задание 10.
Площадь фигуры, задаваемой условиями
x²+y²+2x+10y+10 =<0
x+y+6>=0 равна...?
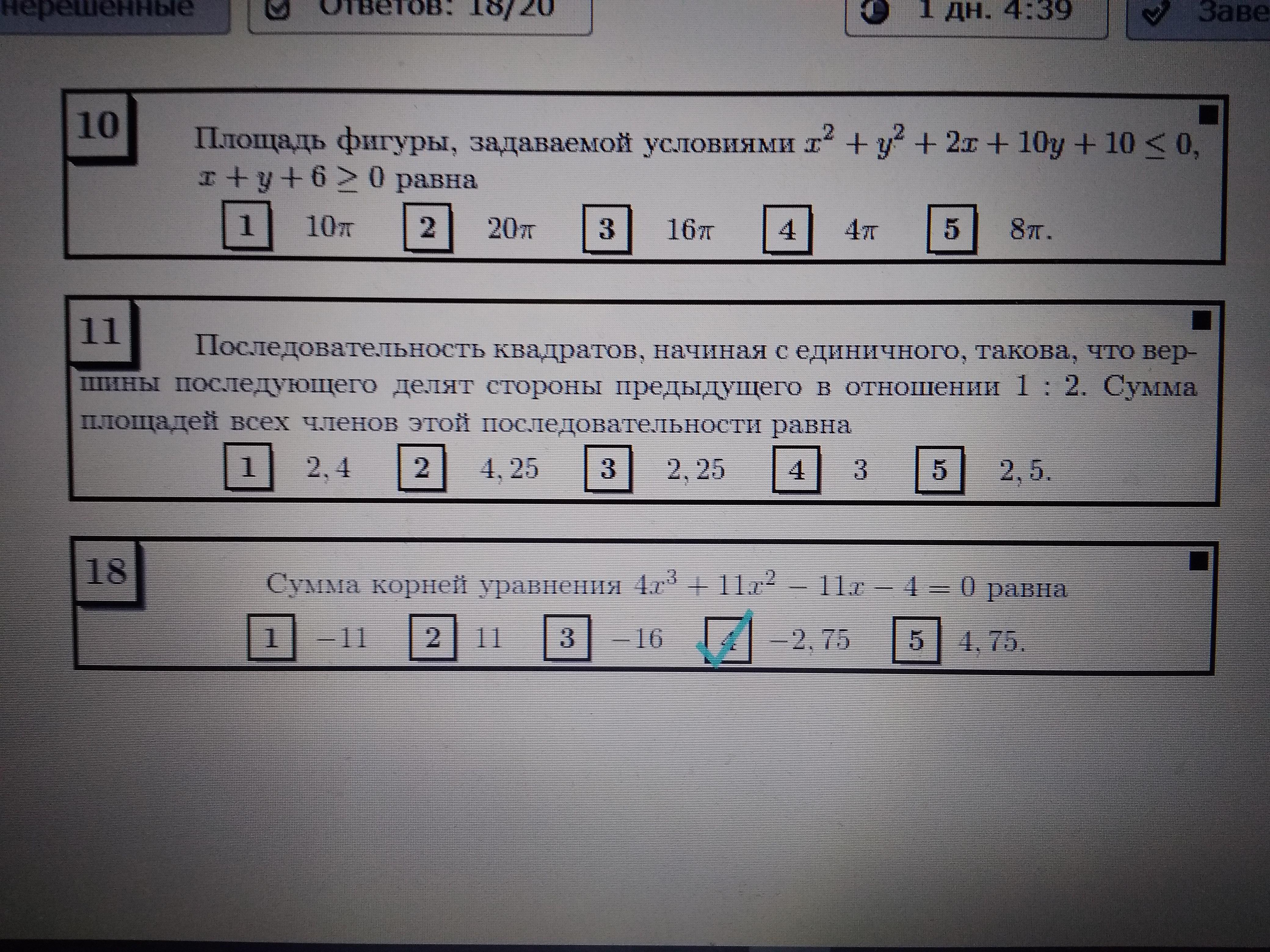
Ответы
https://znanija.com/task/34416108
* * * * * * * * * * * * * * * * * * * *
Ответ: 10) 5 ; 11) 3 ; 12) 4.
Объяснение:
10) x²+y²+2x+10y+10 ≤ 0 ; x+y+6 ≥ 0 x²+y²+2x+10x+10 ≤ 0 ; x+y+6 ≥ 0 ⇔
⇔(x+1)²+(y+5)² ≤ 4² ( круг с центром в точке (-1; -5) и радиусом R=4) ;
y ≥ -x -5 ( область не ниже прямой y = -x -5 , которая проходит через центр окружности (x+1)²+(y+5)² = 4² . Фигура будет полукруг площадь
которой будет S =πR²/2 = π*4²/2 = 8π . ответ : 5
11) S₁= a² =1² = 1 ; S₂ =√( (a/3)²+(2a/3)² ) = 5a²/9 = 5/9 ; ... ⇒ q = 5/9
S =S₁/(1-5/9) =9S₁/4 =9*1/4 = 2,25 . ответ : 3.
12) 4x³+11x²- 11x - 4= 0 ⇔ 4x³- 4 +11x²-11x = 0⇔ 4(x³- 1) +11x(x-1) = 0 ⇔
4(x- 1)(x² +x+1) +11x(x-1) = 0 ⇔ (x- 1)(4(x² +x+1) +11x) = 0⇔4(x- 1)(4x² +15x+4)
сумма корней будет: x₁ +x₂+x ₃ =x₁ +( x₂+x ₃) =1 +(-15/4) = -11/4 = -2,75 .
ответ : 4.