Question

Помогите пожалуйста!!!!!В выпуклом четырёхугольнике ABCD выполнены равенства BC=CD, ∠BAC=∠CAD. Какого из следующих условий достаточно потребовать, чтобы четырёхугольник оказался вписанным?

Выберите все правильные варианты ответа.


AB≠AD

AD>BC

∠BCA>90∘

∠ADC>90∘

∠ABC=90∘

BD не перпендикулярен AC

BD перпендикулярен AC

∠ABC≠∠ADC

∠BCA≠∠ACD

Answer 1

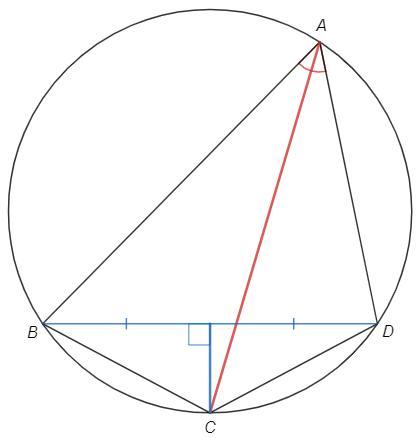
Рассмотрим △BAD.

Дано, что точка С лежит на биссектрисе угла A и серединном перпендикуляре к BD.

Биссектриса и серединный перпендикуляр пересекаются на описанной окружности △BAD (делят дугу BD пополам).

Таким образом, если биссектриса и серединный перпендикуляр НЕ СОВПАДАЮТ, но пересекаются, то точка С лежит на описанной окружности △BAD.

Биссектриса и серединный перпендикуляр не совпадают, если △BAD не равнобедренный (BD - основание).

Достаточные условия:

AB≠AD.

∠BCA>90 (тогда BD не перпендикулярен AC).

BD не перпендикулярен AC.

∠ABC≠∠ADC (тогда ABD≠ADB).

∠BCA≠∠ACD (тогда CA не биссектриса в BCD, следовательно не серединный перпендикуляр).