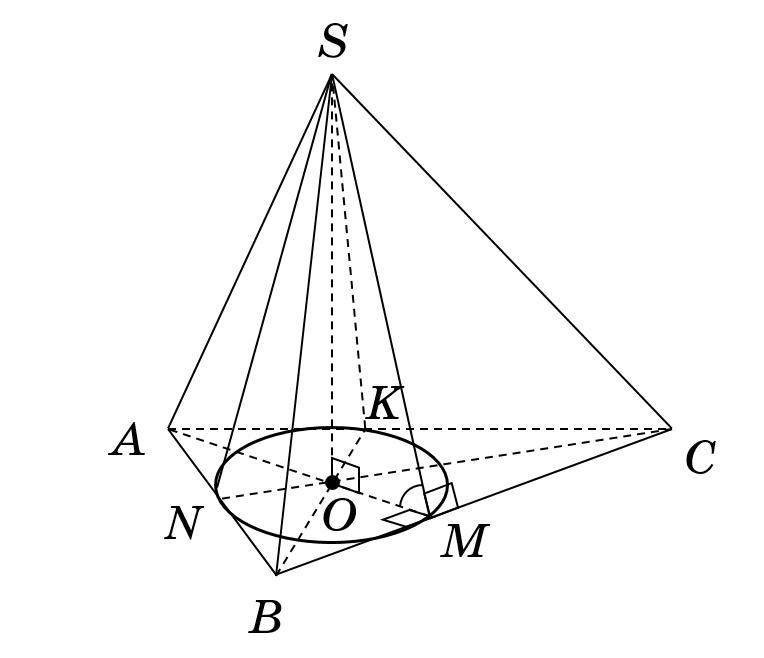
Усі бічні грані піраміди нахилені до основи під кутом 60 градусів. Зайдіть площу бічної поверхні піраміди, якщо її основа - трикутник зі сторонами 12 см, 39 см, і 45 см.
Ответы
Нехай є трикутна піраміда, сторони основи якої см,
см,
см. Якщо всі бічні грані піраміди нахилені до основи під кутом
, то висота
піраміди лежить у центрі
вписаного кола, де
,
та
— радіуси цього кола.
Треба знайти площу бічної поверхні піраміди. Для того щоб її знайти, треба визначити площу кожної бічної грані.
Знайдемо площу основи за формулою Герона:
см — півпериметр основи.
см² — площа основи.
Знайдемо радіус вписаного кола:
см.
Отже, см.
, де
як радіуси вписаного кола, а
та
— дотичні. Тут
— проекції відповідно
на площину
. Отже,
за теоремою про три перпендикуляри. Тому
— лінійні кути двогранного кута відповідно при ребрах
.
Розглянемо прямокутний трикутник
см
(за першою ознакою рівності трикутників
).
Розглянемо трикутник
см²
Розглянемо трикутник
см²
Розглянемо трикутник
см²
Отже, площею бічної поверхні заданої піраміди буде см².
Відповідь: 432 см².