Предмет: Математика,
автор: Dididon1
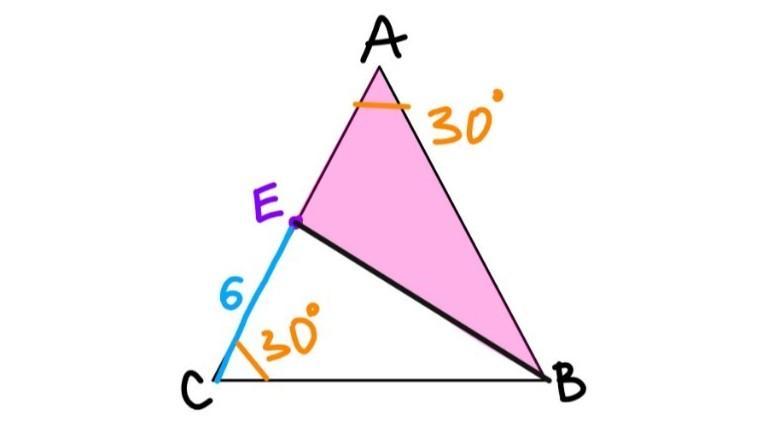
Углы A и C треугольника ABC составляют 30 °, EC = 6 см. Точка E откладывается на сторону AC так, что треугольник ABC подобен треугольнику AEB. Докажите, что треугольник EBC является прямоугольным треугольником. Рассчитайте площадь треугольника ABE. ( Помогите пожалуйста даю 15 баллов)
Ответы
Автор ответа:
1
1)ACB=30°, BAC=30° => ABC равнобедренный => CB=AB
По условию сказано, что треугольники ABC и AEB подобны, они подобны по 1 признаку (2 пропорциональным сторонам и углу между ними)
CB=AB => отношение 1:1 => CE=EA=6
Получаем, что в равнобедренном треугольнике ABC BE выходит из вершины и является медианой => BE еще и высота => треугольник CEB прямоугольный
2) Чтобы найти площадь, нам нужно найти второй катет (высоту BE)
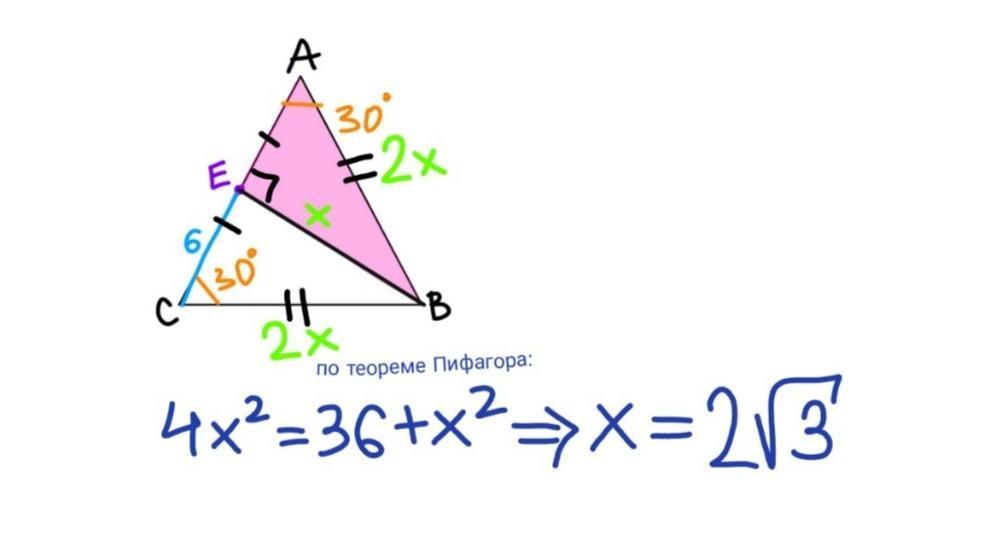
Поскольку катет, лежащий против угла 30° равен половине длины гипотенузы, выражаем BE за х, а AB за 2х
По теореме Пифагора:
4x^2=36+x^2 а значит х=2√3
S(ABE) =0.5×2√3×6=6√3 (шесть корней из трёх)
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: swetochka1sweta
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: Dys9l
Предмет: Алгебра,
автор: Lassyjsjaj
Предмет: Математика,
автор: ДенисШаталов