Предмет: Алгебра,
автор: Oormeero
Помогите найти производную y = е^х ln3x.
Приложения:
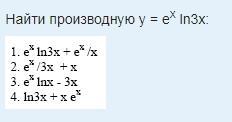
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: samir5
Предмет: Русский язык,
автор: денчик07
Предмет: Русский язык,
автор: 683
Предмет: Химия,
автор: depr
Предмет: Алгебра,
автор: Аноним