Предмет: Алгебра,
автор: minovaksyushashai
ЛОГАРИФМИЧЕСКАЯ СИСТЕМА УРАВНЕНИЙ, С ОДЗ, ПОЖАЛУЙСТА
Приложения:
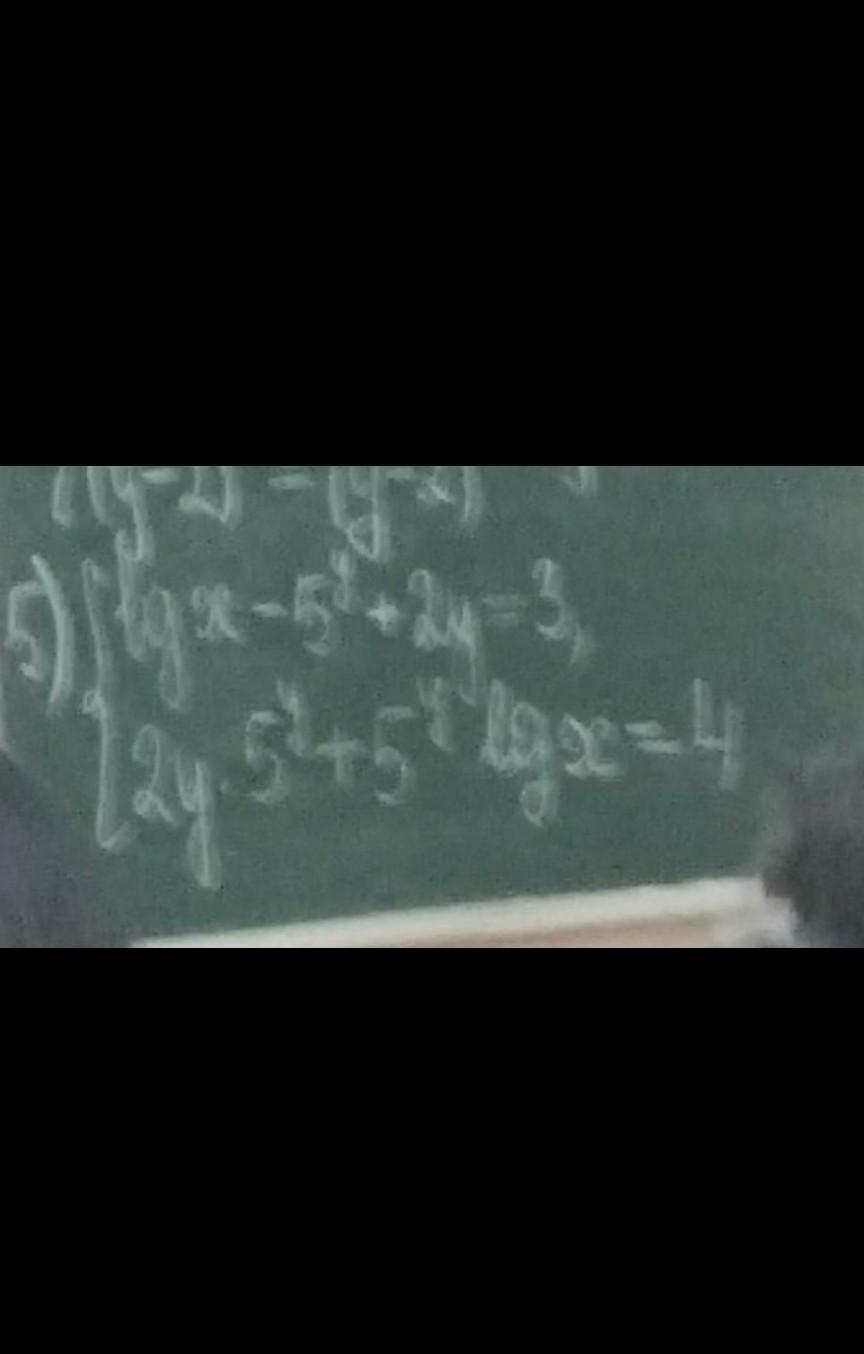
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Одз х>0
Приложения:
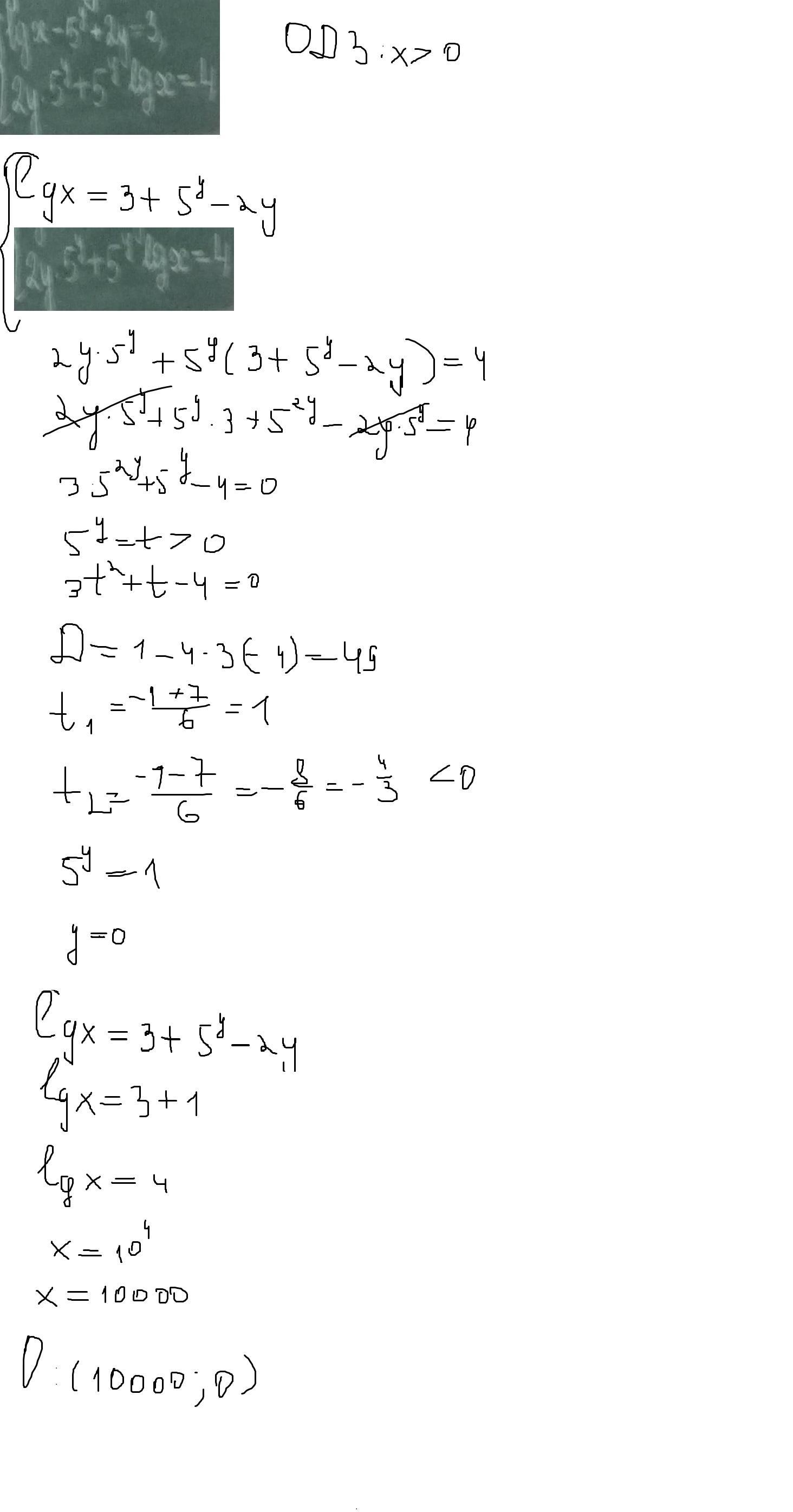
Автор ответа:
1
Похожие вопросы
Предмет: Другие предметы,
автор: briznata
Предмет: Английский язык,
автор: izumrudik
Предмет: Українська мова,
автор: knopa1978
Предмет: Математика,
автор: Lincorn
Предмет: Математика,
автор: elenaElenaVolk