решите пожалуйста 3.1, 5.1, 4
ДАЮ 20 БАЛЛОВ

Ответы
3.1 ТЕОРЕМА : Отношение периметров подобных треугольников равно коэффициенту подобия.
Пусть треугольник ABC подобен треугольнику A₁B₁ C₁ с коэффициентом подобия k. Тогда P₂: P₁ = k
k = 25:10 = 2,5
Следовательно, коэффициент подобия треугольников равен 2,5
Т.к. P₂: P₁ = k то A₁B₁ : AB = k
Поэтому, сторона второго треугольника будет равна:
A₁B₁ = 3*2.5 = 7.5 cм
4. ( прилагаю рис. для лучшего понимания) ТЕОРЕМА : Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
DH : AB = 6:4 = 1,5
DE : BC = 10,5 : 7 = 1,5
EH : AC = 12 : 8 = 1,5
Значит Δ ABC подобен Δ DEH
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Выше было доказано, что треугольники подобны
DE : BC =EH : AC = 1,5
Значит углы, заключенные между этими сторонами, равны.
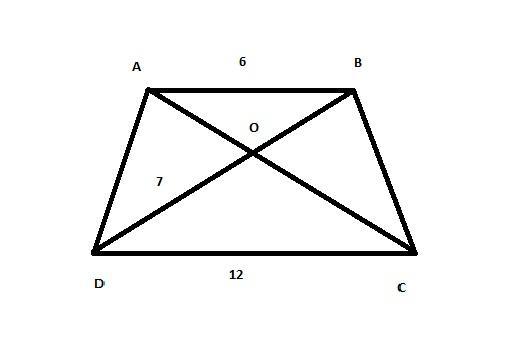
5.1 (прилагаю рис. для лучшего понимания)ТЕОРЕМА: Если 2 угла одного треугольника соответственно равны 2 углам другого, то такие треугольники подобны.
∠ ОАB = ∠ОСD (внутренние накрест лежащие при DС║АB (основания трапеции параллельны между собой) и секущей прямой AC)
∠ OBC = ∠ ODA (внутренние накрест лежащие).
Значит Δ BOА подобен Δ СOD
Отношения сторон в подобных треугольниках равно коэффициенту подобия k
DC : AB = 12:6 = 2
Следовательно DO : OB = 2
OB = 7:2 = 3,5 см