Question

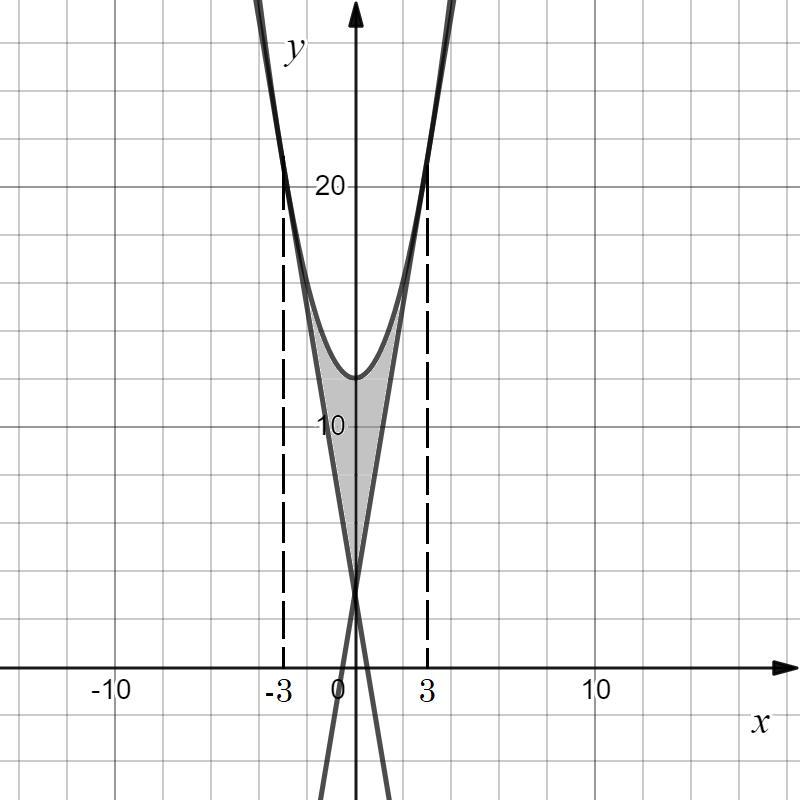
1. Найти площадь фигуры, ограниченной параболой y=x^2+12 и касательными к ней, проведенными из точки A(0;3)
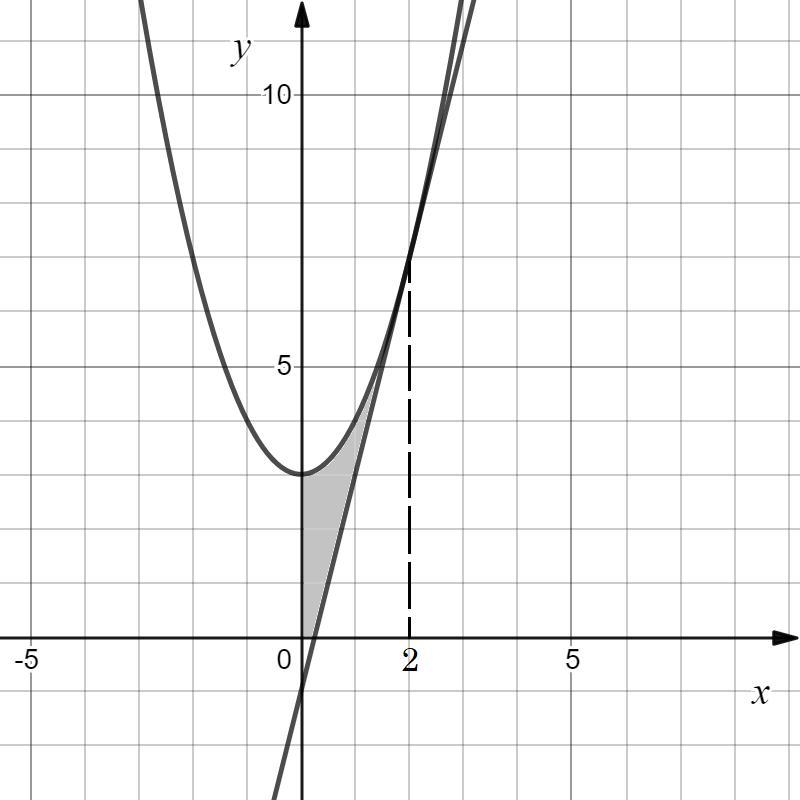
2. Найти площадь фигуры, ограниченной осями координат, параболой y=x^2+3 и касательной к ней в точке A(2;7)

Answer 1

$1. \ y=x^{2} + 12$ — квадратичная функция, графиком которой является парабола с ветвями, направленными вверх. Для построения данной параболы изобразим функцию $y = x^{2}$ и сместим ее на 12 единиц вверх.

Найдем касательные, проведенные к данной функции из точки $A(0; \ 3).$ Касательная имеет формулу линейной функции $y = kx + b$, где коэффициент $b$ — пересечения данной прямой с осью ординат, коэффициент $k$ — угол наклона данной функции относительно оси абсцисс. Как раз точка $A(0; \ 3)$ — точка, которая находится на оси ординат и через которую будут проходить две касательные. Следовательно, $b = 3$ для обеих касательных.

Найдем производную $y' = f'(x_{0})= (x^{2} + 12)' = 2x$ в точке $x_{0}$.

Уравнение касательной для заданной функции имеет вид:

$y = f'(x_{0})(x - x_{0}) + f(x_{0}) = 2x_{0}(x - x_{0}) + x_{0}^{2} + 12 = 2x_{0}x - x_{0}^{2} + 12$

Как известно, коэффициент $b$ данных касательных равен $3.$ Следовательно,

$-x_{0}^{2} + 12 = 3\\x^{2}_{0} = 9\\x_{0} = \pm 3$

Итак, у нас будет две касательных с $x_{0} = -3$ и $x_{0} = 3.$

Найдем касательные, проведенные к функции $y=x^{2} + 12$, используя уравнение касательной. Итак, имеем две касательные:

$1) \ y = 6x + 3\\2) \ y = -6x + 3$

Изобразим все графики функций и найдем площадь фигуры, ограниченной параболой $y=x^{2} + 12$ и касательными, проведенными к ней (см. вложение).

Площадью полученной фигуры будет

$S = \int\limits^{3}_{-3} {(x^{2} + 12)} \, dx - \int\limits^{0}_{-3} {(-6x + 3)} \, dx - \int\limits^{3}_{0} {(6x + 3)} \, dx$

Найдем каждый интеграл по-отдельности:

$\int\limits^{3}_{-3} {(x^{2} + 12)} \, dx = \left(\dfrac{x^{3}}{3} + 12x \right)\bigg|^{3}_{-3} =\dfrac{3^{3}}{3} + 12\cdot 3 - \left(\dfrac{(-3)^{3}}{3} + 12\cdot (-3) \right) =$

$= \dfrac{27}{3} + 36 +\dfrac{27}{3} + 36 = 72 + \dfrac{54}{3} = 72 + 18 = 90$ квадратных единиц.

$\int\limits^{0}_{-3} {(-6x + 3)} = (-3x^{2} + 3x)|^{0}_{-3} = -3\cdot 0^{2} + 3\cdot 0 - (-3\cdot (-3)^{2} + 3\cdot (-3)) =$

$= 0 + 27 + 9 = 36$ квадратных единиц.

Следовательно, $S = 90 - 36 - 36 = 18$ квадратных единиц.

Важно заметить, что мы два раза вычитаем фигуру, образованную пересечением двух касательных и прямой $y = 0$ . Найдем площадь данной фигуры.

Имеем равнобедренный треугольник с основанием $a = 1$ и высотой $h = 3$. Площадью данного треугольника будет $S_{0} = \dfrac{1}{2} \cdot ah = \dfrac{1}{2} \cdot 1 \cdot 3 = 1,5$ квадратных единиц.

Следовательно, окончательной площадью фигуры будет $S' = S + S_{0} = 18 + 1,5 = 19,5$ квадратных единиц

Ответ: $19,5$ квадратных единиц.

$2. \ y = x^{2} + 3$ — квадратичная функция, графиком которой является парабола с ветвями, направленными вверх. Для построения данной параболы изобразим функцию $y = x^{2}$ и сместим ее на 3 единицы вверх.

Оси координат: $y = 0$ и $x = 0$

Найдем касательную функции $y = x^{2} + 3$ в точке с абсциссой $x_{0} = 2$.

Найдем производную $y' =f'(x_{0})= (x^{2} + 3)' = 2x$

Найдем значение производной в точке $x_{0} = 2$: $f'(2) =2 \cdot 2 = 4$

Уравнение касательной для заданной функции имеет вид:

$y = f'(x_{0})(x - x_{0}) + f(x_{0}) = 4 \cdot (x - 2) + 7 = 4x - 8 + 7 = 4x - 1$

Итак, уравнение касательной имеет вид $y = 4x - 1$

Изобразим все графики функций и найдем площадь фигуры, ограниченной параболой $y=x^{2} + 3$, касательной, проведенной к ней, и осями координат (см. вложение).

Площадью полученной фигуры будет

$S = \int\limits^{2}_{0} {(x^{2} + 3)} \, dx - \int\limits^{2}_{0} {(4x - 1)} \, dx = \int\limits^{2}_{0} {(x^{2} + 3 - (4x - 1))} \, dx = \\= \int\limits^{2}_{0} {(x^{2} + 3 - 4x + 1)} \, dx = \int\limits^{2}_{0} {(x^{2} -4x + 4)} \, dx = \left(\dfrac{x^{3}}{3} - 2x^{2} + 4x \right)\bigg|^{2}_{0} =$

$= \dfrac{2^{3}}{3} - 2 \cdot 2^{2} + 4 \cdot 2 - \left(\dfrac{0^{3}}{3} - 2 \cdot 0^{2} + 4 \cdot 0 \right) = \dfrac{8}{3} -8 + 8 - 0 = \dfrac{8}{3}$квадратных единиц.

Ответ: $1\dfrac{2}{3}$ квадратных единиц.