Предмет: Математика,
автор: shestagla
Найти предел
Фото внутри
Приложения:
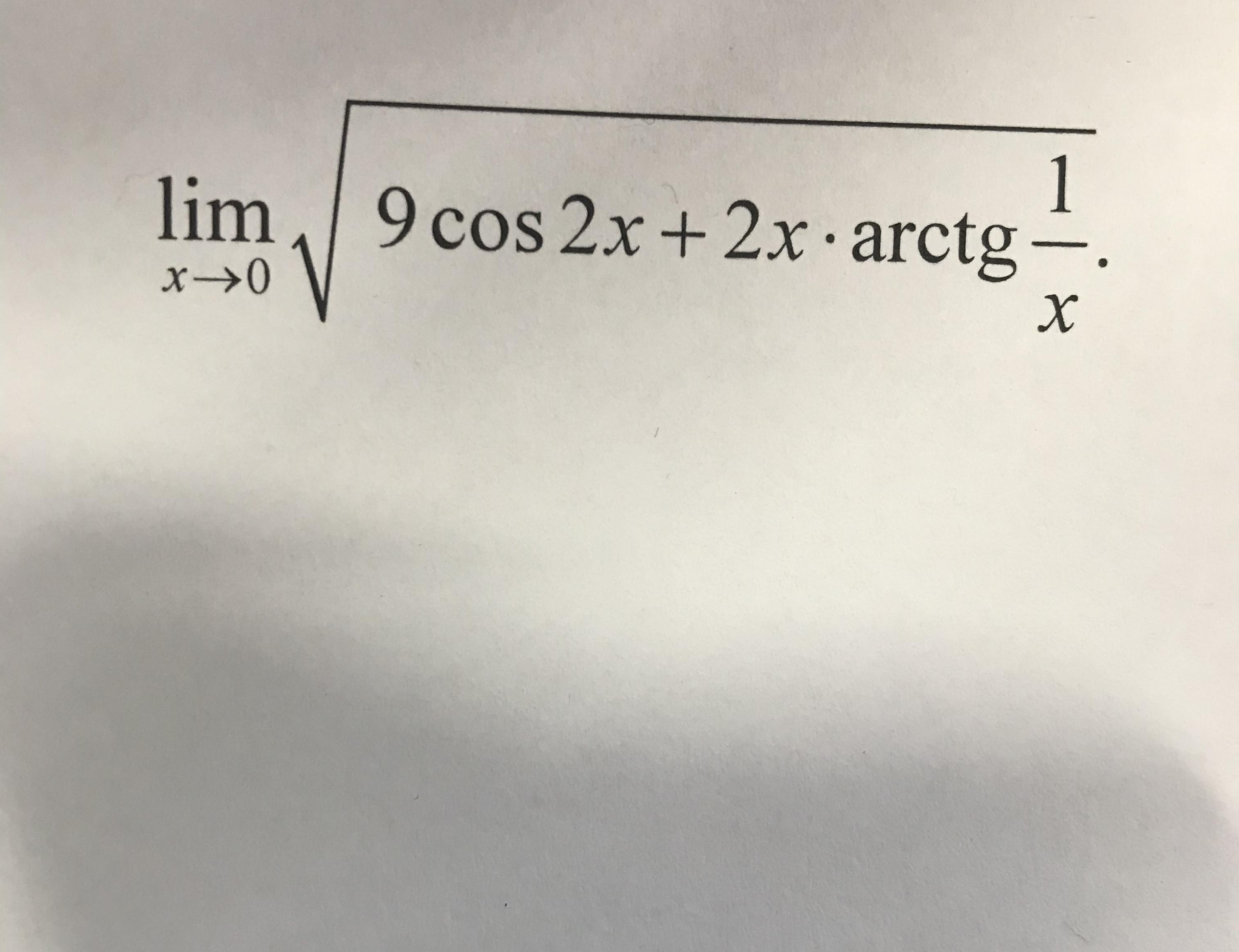
Ответы
Автор ответа:
0
В силу непрерывности функции на области определения,
Тогда:
Похожие вопросы
Предмет: Литература,
автор: ksyhapadlyak123654
Предмет: Математика,
автор: dara39265
Предмет: Математика,
автор: valeriakuleshiva21
Предмет: Алгебра,
автор: Evil322
Предмет: Математика,
автор: умник1005