Question

11 класс.
Вычислить площадь фигуры, ограниченную заданными линиями.
Построить график и найти интеграл. У меня проблема с графиком.
Задания обведены в кружочек)

Answer 1

Ответ: 2) 12 - 5ln 5; 3)7 - 5ln2.

Объяснение:

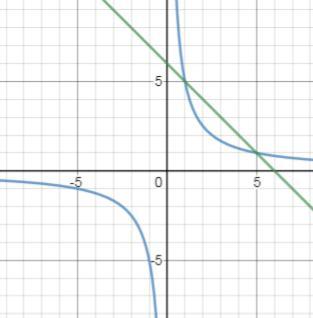
2) График в первом вложении. Во втором вложении заштрихована площадь фигуры, которую нужно найти. Так как нам не дан конкретный отрезок, она ограничивается вертикальными прямыми, проведенными через точки пересечения графиков - х = 1 и х = 5.

График функции y = 6 - x выше графика функции y = 5/x, поэтому формулу площади фигуры составляем следующим образом:

$s=\int\limits^5_1 {(6-x-\frac{5}{x})} \, dx=(6x-\frac{x^2}{2}-5lnx)|^5_1=(6\cdot5-\frac{5^2}{2}-5ln5)-(6\cdot1-\frac{1^2}{5}-5ln1)=30-\frac{25}{2}-5ln5-6+\frac{1}{5}+0=24-\frac{24}{2}-5ln5=24-12-5ln5= 12-5ln5.$

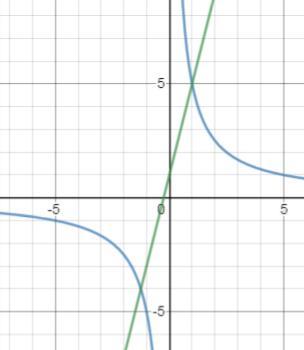
3) График в третьем вложении. В четвертом вложении заштрихована площадь фигуры, которую нужно найти. Так как нам дан только 1 конец отрезка, которым ограничена фигура, вторым концом будет точка пересечения графиков функций - х = 1.

График функции y = 4x + 1 на отрезке [1; 2] выше графика функции y = 5/x, поэтому формулу площади составляем следующим образом:

$S=\int\limits^2_1 {(4x+1-\frac{5}{x})} \, dx=(2x^2+x-5lnx)|^2_1=(2\cdot2^2+2-5ln2)-(2\cdot1^2+1-5ln1)=8+25-ln2-2-1+0=7-5ln2.$