Предмет: Геометрия,
автор: Аноним
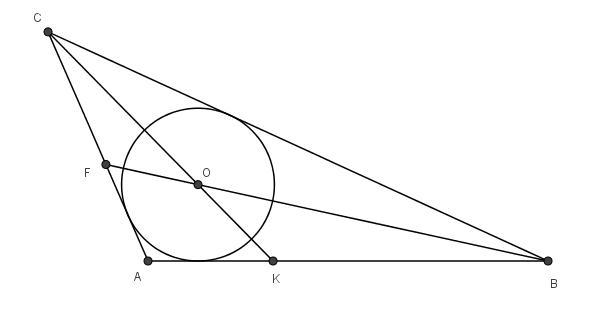
в треугольнике abc известно, что ab= 8 см, bc= 11 см, ac= 5 см. в каком отношении. центр круга, вписаного в треугольник, делит его биссекстрису ck?
Ответы
Автор ответа:
5
Центр вписанной окружности - точка пересечения биссектрис.
Биссектриса угла С делится точкой пересечения биссектрис в отношении (a+b)/c от вершины.
CI/IK = (AC+BC)/AB = (5+11)/8 =2/1
Приложения:

Автор ответа:
6
По свойству биссектрисы :
По теореме Менелая для треугольника ACF:
Ответ: 2 : 1.
Приложения:
Аноним:
Для треугольника ACK
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Биология,
автор: rixxgreg
Предмет: Математика,
автор: pekhtanya2010
Предмет: Математика,
автор: иван0077
Предмет: Физика,
автор: yuriyosipov20