Предмет: Математика,
автор: sanekbikbulatov
Найдите предел последовательности: xn=5n/6n-2 + 1/n cos n.
Приложения:
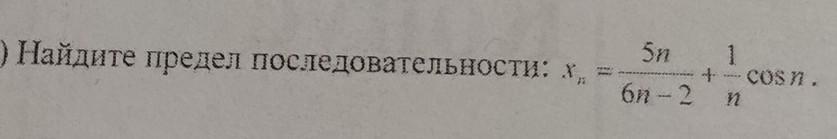
Ответы
Автор ответа:
1
- ограниченная последовательность
- бесконечно малая последовательность
Тогда как произведение бесконечно малой и ограниченной последовательностей.
Похожие вопросы
Предмет: Окружающий мир,
автор: sonzelana020275
Предмет: Алгебра,
автор: Аноним
Предмет: Информатика,
автор: sonaokuneva189
Предмет: Математика,
автор: ArtemCheat
Предмет: Математика,
автор: малик20063