Предмет: Алгебра,
автор: deniskot730
5 теме «Квадратные уравнения »
Вариант 2
1. Решите уравнение:
а) 3х - 15 = (0);
б) х*+ 7x = 0);
в) 12х2 - 5x - 2 = 0;
г) х“ - 6x - 16 = 0;
д) х - 3x + 11 = ()
е) (3х - 1)(3x+1) - (х - 1)(х + 2) = 8.
Ответы
Автор ответа:
4
полное условие во вложении
_________________________
Ответ:
Ответ: -7; 0
Ответ: -0,25; 2/3
Ответ: -2; 8
Ответ:
Ответ: -0,875; 1
Приложения:
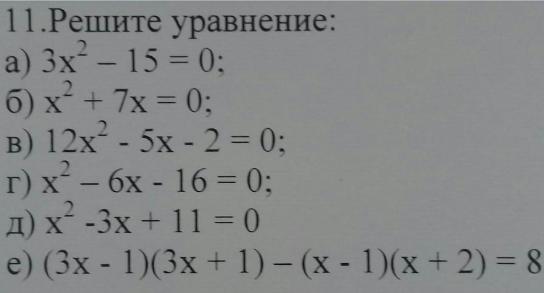
Похожие вопросы
Предмет: Математика,
автор: metroroyale2000
Предмет: Математика,
автор: nikayaxta
Предмет: Беларуская мова,
автор: nightcor4kso2
Предмет: Математика,
автор: ysj
Предмет: Математика,
автор: 78dekhanova