Предмет: Алгебра,
автор: gozer10
Я нашел корни 2 и 6, а вот как правильно все это дело записать я не знаю.
Приложения:
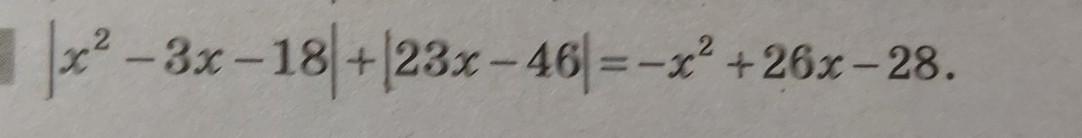
Ответы
Автор ответа:
1
Ответ:
Любой х из отрезка [2,6]
Объяснение:Перепишем так:
|(x-6)*(x+3)+23*|x-2|=-x^2+26х-28
Пусть х меньше либо равен 6 но больше либо равен -3
-х^2+3х+18+23*|x-2|=-x^2+26х-28
23*|x-2|=23х-46
При х больше либо равном 2 это верно всегда, а при х меньше 2 не верно.
Значит одно множество решений 6>=х>=2
Пусть теперь х больше 6 или х меньше -3
х^2-3х-18+23*|x-2|=-x^2+26х-28
2х^2-29x+10=-23*|x-2|
Пусть х больше 6 Тогда 2х^2-29x+10=-23*x+46
2х^2-29x+10=-23*x+46
2х^2-6x-36=0
х^2-3x-18=0 х=-3 или х=6 Оба решения вне интервала
Пусть х меньше -3
2х^2-29x+10=23*x-46
2x^2-62x+56=0
x^2 -31x+28=0
x1=0,5*(31+sqrt(849)) x2=0,5*(31-sqrt(841))
Оба корня больше -3.
Значит только первое множество решений и есть ответ.
gozer10:
спасибо !^^
Вы правы, спасибо.
Это из 23*|x-2|=23х-46 сразу. Изменил.
Автор ответа:
1
Ответ [2;6]
Решение задания приложено.
Приложения:

спасибо, вроде разобрался ^^
Похожие вопросы
Предмет: Українська література,
автор: denisdmitruk093
Предмет: Українська мова,
автор: ninaserman0
Предмет: Алгебра,
автор: milananazarova277
Предмет: Математика,
автор: kitichenkodawid1910