Предмет: Математика,
автор: vlada20041985
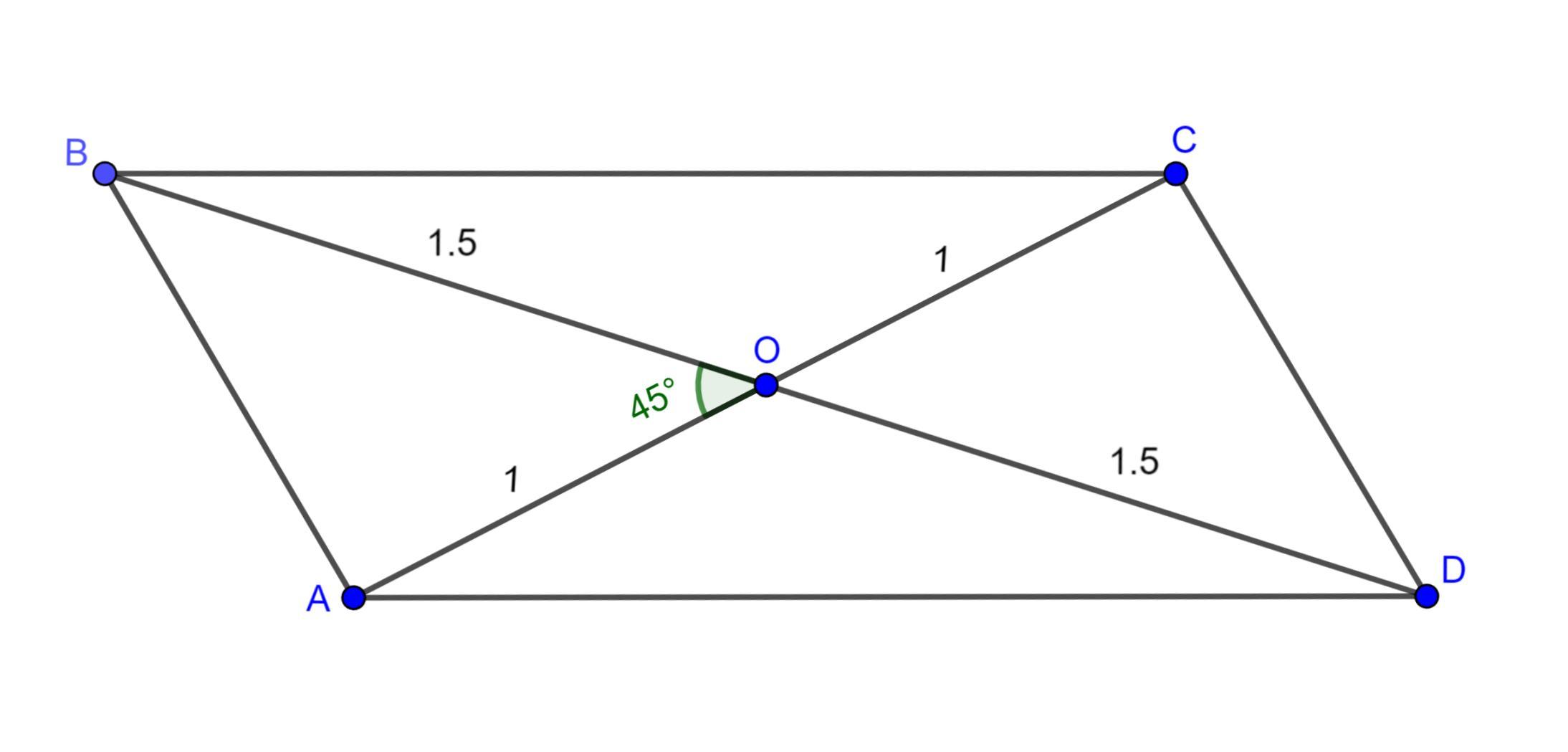
В параллелограмме диагонали равны 2дм и 3дм а угол между ними-45 градусов . Найдите с точностью до 0,01 дм стороны параллелограмма
Ответы
Автор ответа:
62
Дано:
ABCD - параллелограмм
AC = 2 дм
BD = 3 дм
∠BOA = 45°
Найти: AB, BC, CD, DA с точностю до 0.01 дм.
Решение: В параллелограмме диагонали пересекаются, и точкой пересечения делятся пополам ⇒ AO = OC = AC / 2 = 1 дм и BO = OD = BD / 2 = 1.5 дм
Рассмотрим ΔABO
Найдём сторону AB с помощью теоремы косинусов:
a = AO, b = BO, c = AB, cos ∠ab = cos ∠BOA
Рассмотрим ΔBOC
∠BOA и ∠BOC - смежные ⇒ ∠BOA + ∠BOC = 180° ⇒ ∠BOC = 180° - ∠BOA = 180° - 45° = 135°
Найдём BC по теореме косинусов:
c = BC, a = BO, b = CO, cos ∠ab = cos ∠BOC
В параллелограмме стороны попарно равны ⇒ CD = AB ≈ 1.07 дм и DA = BC ≈ 2.31 дм
Ответ: 1.07 дм, 2.31 дм, 1.07 дм, 2.31 дм
Приложения:
Похожие вопросы
Предмет: Биология,
автор: fpxuyiduyduyfih
Предмет: Математика,
автор: nurlan100206
Предмет: Английский язык,
автор: bananikbananik819
Предмет: Математика,
автор: NastyaKotMur
Предмет: Алгебра,
автор: gt60