Предмет: Алгебра,
автор: eleavious
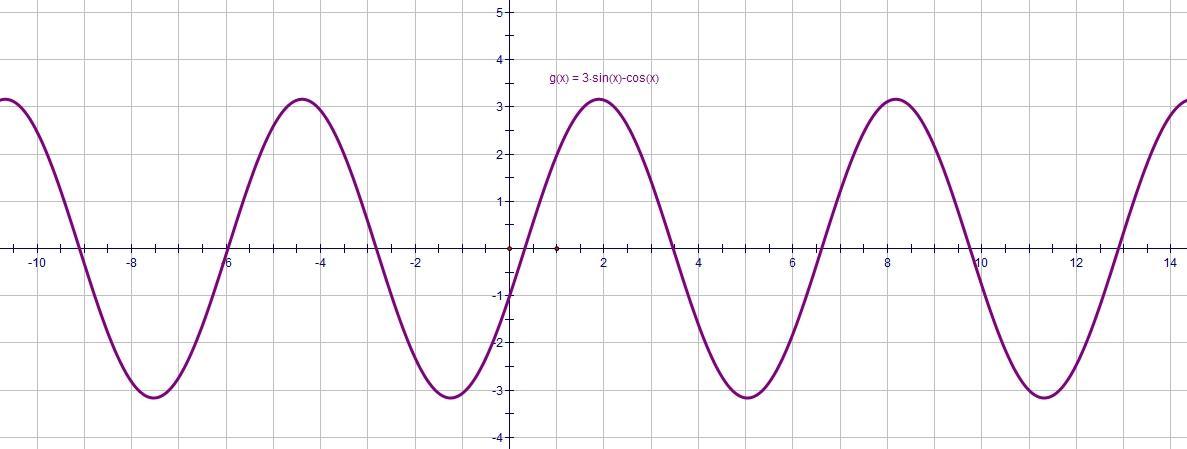
Найдите наибольшее значение выражения: 3sinα−cosα
Ответы
Автор ответа:
11
Ответ:
√10
Пошаговое решение:
Приложения:

Автор ответа:
8
Ответ: (на картинке)
Объяснение:
искать ответ можно разными способами...
удобнее всего использовать производную
(но, возможно, эту тему еще не проходили...
не указано-для какого класса задание)))
f ' (x) = 3cos(x)+sin(x)
f ' (x) = 0 условие для нахождения экстремума...
3cos(x)+sin(x)=0
однородное уравнение первой степени:
делим обе части равенства на cos(x)≠0
tg(x) = -3 ---> x = -arctg(3) + πk, k∈Z
если tg(x)=-3 --> sin(x) = -3cos(x)
(-3cos(x))² + cos²(x) = 1
cos²(x) = 0.1 --> 1) cos(x) = √0.1 или 2) cos(x) = -√0.1
тогда 1) sin(x) = -3√0.1 или 2) sin(x) = 3√0.1
значения функции:
1) 3sin(x)-cos(x) = -9√0.1-√0.1 = -10√0.1 = -√10 ≈≈ -3.16 это minimum
2) 3sin(x)-cos(x) = 9√0.1+√0.1 = 10√0.1 = √10 ≈≈ 3.16 это maximum
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: varchun83
Предмет: Математика,
автор: oluh228
Предмет: Математика,
автор: romaniuk2003vika
Предмет: Математика,
автор: чонай
Предмет: Математика,
автор: idoroch