Предмет: Алгебра,
автор: vodopianovvad
ПОМОГИТЕ ПОЖАЛУЙСТА!!!
log3x^3+log2x^2=2lg6/lg2+1
Приложения:
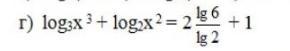
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Алгебра,
автор: 10azimm
Предмет: Английский язык,
автор: CoralineBeautiful
Предмет: Физика,
автор: Hiskbdk
Предмет: Математика,
автор: tsoy1969