Предмет: Геометрия,
автор: DimasPlay31
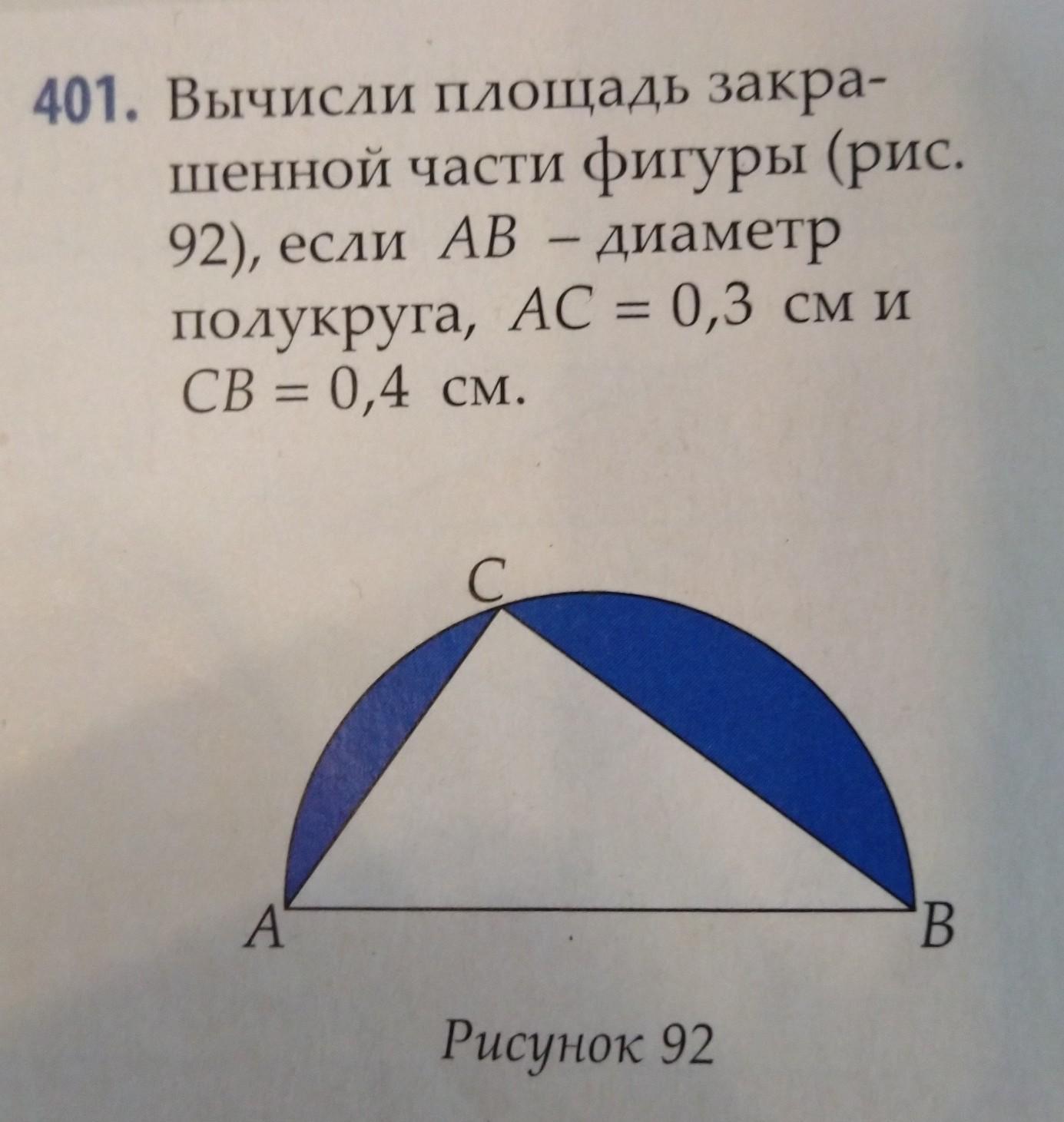
Вычисли площадь закрашенной части фигуры (рис. 92), если AB - диаметр полукруга, AC = 0,7 см и CB = 0,4 см.
Приложения:
Simba2017:
треугольник прямоугольный
из полукруга вычти площадь треугольника
Ответы
Автор ответа:
0
Угол С опирается на диаметр АВ, следовательно , этот угол С является прямым. Площадь прямоугольного треугольника равна AC*BC/2=0,7*0,4/2=0,14 см².
По теореме Пифагора : AB² = 0,7² + 0,4² = 0,65 отсюда AB = √0,65 см. Тогда R = 0,5√0,65 см.
Площадь полукруга : πR²/2 = 65π/8 см².
Площадь закрашенной части фигуры: S = (65π/8) - 0,14 см²
Похожие вопросы
Предмет: Химия,
автор: mrtimckuck
Предмет: Английский язык,
автор: gulibonurahmatova
Предмет: Английский язык,
автор: mamedovorxan87
Предмет: Математика,
автор: zvezda771rus