Предмет: Математика,
автор: dukanov2001
Найти производную функции
Приложения:
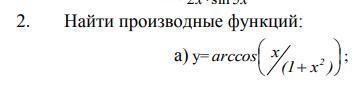
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: emiliazhelonkina30
Предмет: Окружающий мир,
автор: pogodinaludmila
Предмет: Математика,
автор: Славик226
Предмет: Математика,
автор: Nikakorotkova4