Предмет: Геометрия,
автор: 12cerberuss
В каждом надо решить Б
Приложения:

drakerton:
как переводится задание в 233?
и в двух остальных желательно тоже перевод
трикутник-треугольник
довжина-длинна
перетин-пересечение
рівняння- уравнение
обчисліть- вычислите
Ответы
Автор ответа:
0
Ответ:
233 б) Медиана соединяет вершину треугольника с серединой противолежащей стороны. Следовательно, при решении задачи составления уравнения медианы нужно:
1) Найти координаты середины отрезка по координатам его концов.
2) Составить уравнение прямой, проходящей через две точки: найденную середину отрезка и противолежащую вершину.
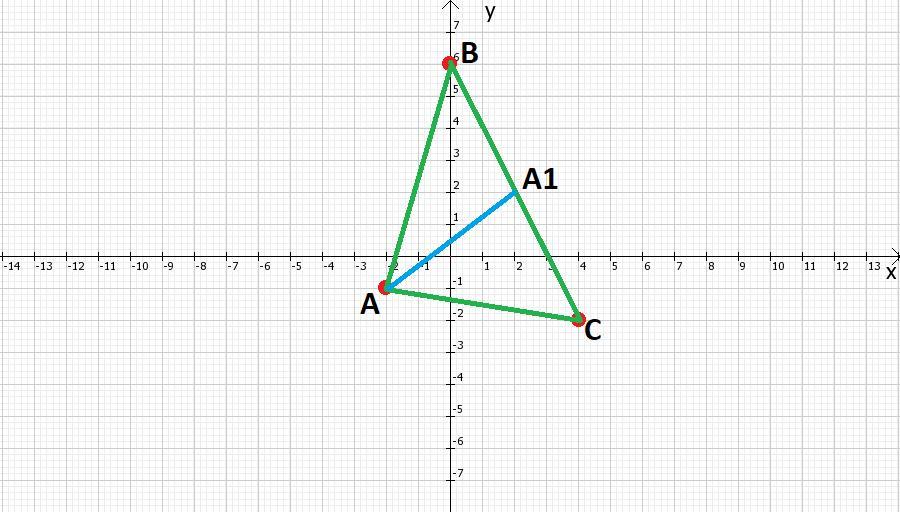
2) Уравнение медианы AA₁ будем искать в виде y=kx+b.
Найдём уравнение прямой, проходящей через точки A(-1;1) и A1(2;3). Составляем и решаем систему уравнений:
Отсюда получаем, что , а
Уравнение медианы AA₁:
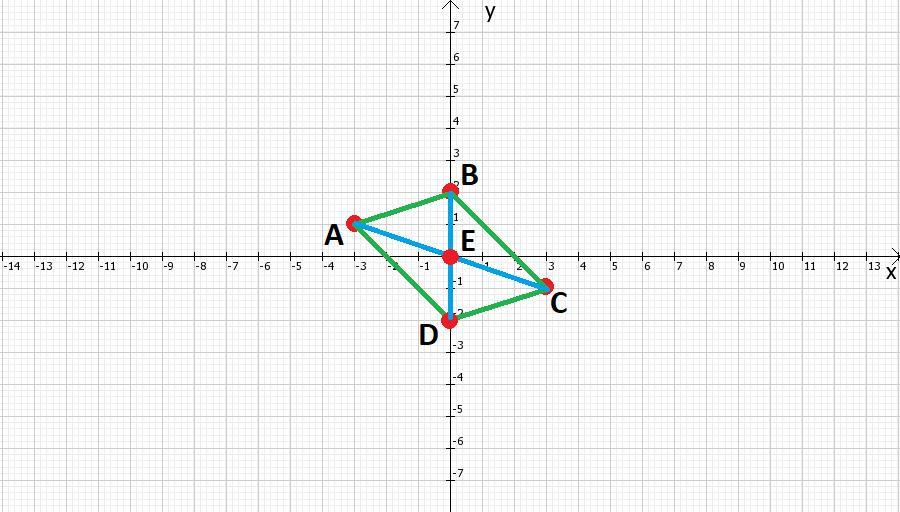
234б) Координаты точки D (0; -2). Координаты точки пересечения диагоналей: (0; 0)
235б)
Итак, А₁(2;2).
cм
Приложения:

Похожие вопросы
Предмет: Математика,
автор: Sofiiastoliar
Предмет: География,
автор: Firttixxx
Предмет: Математика,
автор: Sofiiastoliar
Предмет: Биология,
автор: alfred54
Предмет: Биология,
автор: Dimas10801